题目内容
2.已知(x2+y2+1)(x2+y2+3)=8.则x2+y2的值为1.分析 设x2+y2=a,把原方程化为关于a的一元二次方程,解方程求出a,根据非负数的性质判断即可.
解答 解:设x2+y2=a,
原方程变形为:(a+1)(a+3)=8,
即a2+4a-5=0,
解得,a1=1,a2=-5,
∵x2+y2≥0,
∴x2+y2=1,
故答案为:1.
点评 本题考查的是一元二次方程的解法,掌握配方法解一元二次方程的一般步骤、非负数的性质是解题的关键.

练习册系列答案
相关题目
 如图,在?ABCD中,对角线BD、AC交于点O,∠ABD=2∠DBC,AE⊥BD于E.探究线段AB与OE的数量关系.
如图,在?ABCD中,对角线BD、AC交于点O,∠ABD=2∠DBC,AE⊥BD于E.探究线段AB与OE的数量关系. 如图,已知HM平分∠EHD,GB∥HD,∠3=35°.
如图,已知HM平分∠EHD,GB∥HD,∠3=35°.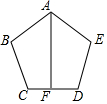 如图,已知AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点,连接A,F.AF与CD有怎样的关系?并说明理由.
如图,已知AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点,连接A,F.AF与CD有怎样的关系?并说明理由.