Question

如图，在直角梯形ABCD中，CD⊥AD，BC∥AD，AD=AB=10cm，BC=4cm．点P自点D出发以每秒1cm的速度沿DA向点A移动，点Q自点A出发以每秒

15

16

cm的速度沿AB向点B移动，点P、Q同时出发，当点P到达点A时，点Q随之停止．设点P、Q运动的时间为t（s）（o≤t≤10）．
（1）求CD的长；
（2）在点P、Q的运动过程中，设△PAQ的面积为y，求y与t的函数关系式；
（3）在运动过程中，△PAQ的面积能否是梯形ABCD面积的

5

8

？若能，求出t的值；若不能，请说明理由；
（4）t为何值时，△PAQ是直角三角形．

Answer 1

考点：四边形综合题

专题：

分析：（1）作BE⊥AD，则四边形BCDE为矩形，根据勾股定理即可求得BE的长，即可解题；
（2）易求AP和AQ的长，根据三角形计算公式S=

1

2

ab•sinC即可解题；
（3）求出y关于t的解析式，易求梯形ABCD面积，即可求得梯形ABCD面积的

5

8

，解一元二次方程即可解题；
（4）分类讨论①当∠APQ=90°时，②当∠AQP=90°时，根据cosA=

3

5

即可解题．

解答：解：（1）作BE⊥AD，则四边形BCDE为矩形，

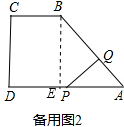
∴DE=BC=4cm，
∵AD=10cm，
∴AE=6cm，
根据勾股定理可得BE²=AB²-AE²=64cm²，
∴CD=BE=8cm；
（2）∵BE=8，AB=10，
∴sinA=

4

5

，
∵t秒后AP=AD-DP=10-t，AQ=

15

16

t，
∴△PAQ的面积为y=

1

2

AP•AQ•sinA=

3

8

t（10-t）=-

3

8

t²+

15

4

t；
（3）∵S_梯形ABCD=

1

2

（AD+BC）•CD=56，
∴y=-

3

8

t²+

15

4

t=

5

8

×56=35，
解得：t无解，故不存在；
（4）cosA=

6

10

=

3

5

，
①当∠APQ=90°时，即10-t=

3

5

×

15

16

t时，
解得：t=

32

5

，
②当∠AQP=90°时，即

3

5

（10-t）=

15

16

t时，
解得：t=

100

41

，
故t为

32

5

或

100

41

时，△PAQ是直角三角形．

点评：本题考查了一次函数的综合应用，考查了一元二次方程的求解，考查了三角函数在直角三角形中运用，本题求得sinA，cosA是解题的关键．