题目内容
 如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=8,ON,CD分别为两圆的半径,求阴影部分的面积.
如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=8,ON,CD分别为两圆的半径,求阴影部分的面积.考点:切线的性质,勾股定理,垂径定理
专题:
分析:如图,作OE⊥MN于E,易得四边形DCOE为矩形,再根据垂径定理得到ME=NE=
MN,在Rt△OEN中,利用勾股定理得到ON2-OE2=EN2,然后利用阴影部分的面积=
S⊙O-
S⊙C-进行计算.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解解:如图,作OE⊥MN于E.
∵大半圆的弦AB与小半圆相切,
∴CD为⊙C的半径,
∴OC⊥MN,
又∵MN∥AB,
∴四边形DCOE为矩形,
∴OE=CD,
∵OE⊥MN,
∴ME=NE=
MN=
×8=4,
在Rt△OEN中,ON2-OE2=EN2=16,
∵阴影部分的面积=
S⊙O-
S⊙C=
(π•ON2-π•CD2)=
π×16=8π.
∵大半圆的弦AB与小半圆相切,
∴CD为⊙C的半径,
∴OC⊥MN,
又∵MN∥AB,
∴四边形DCOE为矩形,
∴OE=CD,
∵OE⊥MN,
∴ME=NE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OEN中,ON2-OE2=EN2=16,
∵阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了圆的切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目

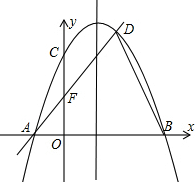 已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A,B,点B(4,0),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).
已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A,B,点B(4,0),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).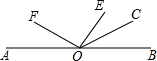 如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为
如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为 如图,数轴上A,B,C三点所表示的有理数的和是
如图,数轴上A,B,C三点所表示的有理数的和是