题目内容
(1)如图1,点C、D在线段AB上,△PCD是等边三角形,且∠APB=120°,求证:△ACP∽△PDB;
(2)如图2,点C、D在线段AB上,△PCD是等腰三角形,且PC=PD,若∠APC=∠B,AC=2,BD=6,你能求出等腰三角形△PCD的腰长吗?
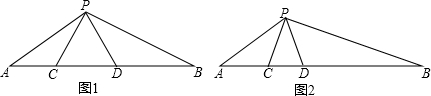
(2)如图2,点C、D在线段AB上,△PCD是等腰三角形,且PC=PD,若∠APC=∠B,AC=2,BD=6,你能求出等腰三角形△PCD的腰长吗?

考点:相似三角形的判定与性质
专题:
分析:(1)如图1,证明∠A=∠BPD,∠APC=∠B,即可解决问题.
(2)如图2,证明∠A=∠BPD,结合∠APC=∠B,得到△ACP∽△PBD,列出比例式即可解决问题.
(2)如图2,证明∠A=∠BPD,结合∠APC=∠B,得到△ACP∽△PBD,列出比例式即可解决问题.
解答: 解:(1)如图1,∵△PCD是等边三角形,
解:(1)如图1,∵△PCD是等边三角形,
∴∠PCD=∠CPD=60°,
∠A+∠APC=∠PCD=60°;
∵∠APB=120°,
∴∠APC+∠BPD=120°-60°=60°,
∴∠A=∠BPD;
同理可证:∠APC=∠B,
∴△ACP∽△PDB.
(2)如图2,∵PC=PD,
∴∠PCD=∠PDC;
∵∠A+∠APC=∠PCD,∠B+∠BPD=∠PDC,
且∠APC=∠B,
∴∠A=∠BPD;
∴△ACP∽△PBD,
∴PC:BD=AC:PD,而PC=PD,
∴PC2=AC•BD=2×6,
∴PC=2
.
 解:(1)如图1,∵△PCD是等边三角形,
解:(1)如图1,∵△PCD是等边三角形,∴∠PCD=∠CPD=60°,
∠A+∠APC=∠PCD=60°;
∵∠APB=120°,
∴∠APC+∠BPD=120°-60°=60°,
∴∠A=∠BPD;
同理可证:∠APC=∠B,
∴△ACP∽△PDB.
(2)如图2,∵PC=PD,
∴∠PCD=∠PDC;
∵∠A+∠APC=∠PCD,∠B+∠BPD=∠PDC,
且∠APC=∠B,
∴∠A=∠BPD;
∴△ACP∽△PBD,
∴PC:BD=AC:PD,而PC=PD,
∴PC2=AC•BD=2×6,
∴PC=2
| 3 |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深入观察探究、大胆猜测推理、科学求解论证.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
有五根木棒,它们的长度分别为2cm、6cm、8cm、10cm、12cm,从中取出三根首尾顺次连接搭成一个直角三角形,则这三根木棒的长度分别为( )
| A、2cm、6cm、8cm |
| B、6cm、8cm、10cm |
| C、6cm、8cm、12cm |
| D、2cm、8cm、10cm |
 如图,O是△ABC的角平分线的交点,△ABC的面积为2,周长是4,则O到BC的距离是
如图,O是△ABC的角平分线的交点,△ABC的面积为2,周长是4,则O到BC的距离是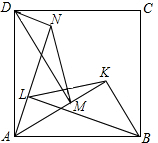 如图,在正方形ABCD中,AK、AN是∠A内的两条射线,BK⊥AK,BL⊥AN,DM⊥AM,DN⊥AN,求证:KL=MN,KL⊥MN.
如图,在正方形ABCD中,AK、AN是∠A内的两条射线,BK⊥AK,BL⊥AN,DM⊥AM,DN⊥AN,求证:KL=MN,KL⊥MN.
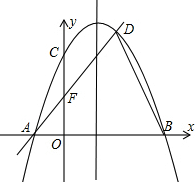 已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A,B,点B(4,0),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).
已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A,B,点B(4,0),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).