题目内容
证明:任意14个连续正整数中,必有一个数不是2、3、5、7、11中任何一个数的倍数.
考点:约数与倍数
专题:
分析:根据题意得出14个连续的正整数,7奇7偶,再利用7的倍数,11的倍数以及3,5的倍数的特征分析得出答案.
解答:证明:∵14个连续的正整数,7奇7偶.
∴7个偶数被2整除,只须考虑7个奇数,
不妨设为 x-6,x-4,x-2,x,x+2,x+4,x+6
很显然,这7个数中,
被7整除的最多只有一个,
被11整除的最多也只有一个.
被3整除的最多有3个(x-6,x,x+6)
被5整除的最多有2个 (x-6,x+4 或 x-4,x+6)
这样,1+1+3+2=7个,
但由于 x-6,x,x+6 与 x-6,x+4 或 x-4,x+6中 必有一数相同,
故“这7个数”是无法实现都是3、5、7、11的倍数,
因此,任意14个连续正整数中,必有一个数不是2、3、5、7、11中任何一个数的倍数.
∴7个偶数被2整除,只须考虑7个奇数,
不妨设为 x-6,x-4,x-2,x,x+2,x+4,x+6
很显然,这7个数中,
被7整除的最多只有一个,
被11整除的最多也只有一个.
被3整除的最多有3个(x-6,x,x+6)
被5整除的最多有2个 (x-6,x+4 或 x-4,x+6)
这样,1+1+3+2=7个,
但由于 x-6,x,x+6 与 x-6,x+4 或 x-4,x+6中 必有一数相同,
故“这7个数”是无法实现都是3、5、7、11的倍数,
因此,任意14个连续正整数中,必有一个数不是2、3、5、7、11中任何一个数的倍数.
点评:此题主要考查了约数与倍数,正确把握倍数的特征进而分析得出是解题关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
实数a、b在数轴上分别对应A、B两点,A点在原点左侧,B点在原点右侧,且|a|<|b|,则
的值是( )
| a-b |
| a+b |
| A、大于0 | B、小于0 |
| C、等于0 | D、不能确定 |

 在△ABC中,CP平分∠ACB,BP是△ACE的角平分线,∠A=50°,求∠P的度数.
在△ABC中,CP平分∠ACB,BP是△ACE的角平分线,∠A=50°,求∠P的度数.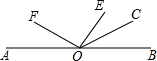 如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为
如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为