题目内容
18.计算:(1)(2$\sqrt{48}$-$\sqrt{75}$+3$\sqrt{12}$)+$\sqrt{3}$
(2)($\sqrt{3}$-$\sqrt{2}$)2(5+2$\sqrt{6}$)
分析 (1)先对括号内的二次根式化简,再合并同类项即可解答本题;
(2)根据完全平方差公式和平方差公式可以解答本题.
解答 解:(1)(2$\sqrt{48}$-$\sqrt{75}$+3$\sqrt{12}$)+$\sqrt{3}$
=$8\sqrt{3}-5\sqrt{3}+6\sqrt{3}+\sqrt{3}$
=10$\sqrt{3}$;
(2)($\sqrt{3}$-$\sqrt{2}$)2(5+2$\sqrt{6}$)
=$(3-2\sqrt{6}+2)•(5+2\sqrt{6})$
=$(5-2\sqrt{6})(5+2\sqrt{6})$
=25-24
=1.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式的混合运算的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字-2,-1,0;从甲袋中随机抽取一个小球,再从乙袋中随机抽取一个小球,两球数字之和为1的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
3.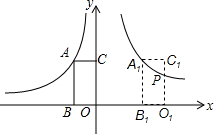 如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上.将矩形向右平移6个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,边C1O1与此图象交于点P,则点P的纵坐标为( )
如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上.将矩形向右平移6个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,边C1O1与此图象交于点P,则点P的纵坐标为( )
 如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上.将矩形向右平移6个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,边C1O1与此图象交于点P,则点P的纵坐标为( )
如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上.将矩形向右平移6个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,边C1O1与此图象交于点P,则点P的纵坐标为( )| A. | $\frac{3}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{2}$ | D. | $\frac{8}{3}$ |
8.下列图案中,既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
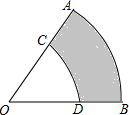 如图,已知扇形OAB与扇形OCD是同心圆,OA=R,OC=r.
如图,已知扇形OAB与扇形OCD是同心圆,OA=R,OC=r.