题目内容
10.如图1,E、F分别是正方形ABCD的边AB、AD的中点,且AB=2,若将△AEF绕点A逆时针旋转一周,在旋转过程中直线BE、DF相交于点P.(1)在△AEF绕点A逆时针旋转过程中,线段BE、DF有怎样的数量关系和位置关系,并就图2的位置加以说明;
(2)在△AEF绕点A逆时针旋转过程中,线段PA的长度是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求当△AEF绕点A从起始位置旋转一周回到终止位置过程中,点P运动的路径长.

分析 (1)由旋转得到∠BAE=∠DAF,AB=AD,AE=AF,判断出△ABE≌△ADF,再利用互余判断出垂直.
(2)利用直角三角形的性质求出PH,AH,再得到最大PA,
(3)先判断出P在以O圆心,$\sqrt{2}$为半径的圆上,再计算即可.
解答 解:(1)BE=DF,BE⊥DF,如图1,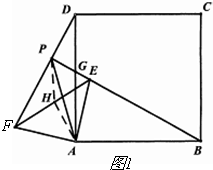
在△ABE和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAF}\\{AE=AF}\end{array}\right.$
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ABE+∠AGB=90°,
∴∠ADF+∠PGD=90°,
∴∠DPG=90°,
∴BE⊥DF;
(2)如图1,
取EF中点,连接PH,AH,
∵∠EAF=∠FPE=90°,
∴PH=AH=$\frac{1}{2}$EF=$\frac{\sqrt{2}}{2}$,
∴点P,H,A三点共线时,PA最长为$\sqrt{2}$.
(3)连接BD,取BD中点O,连接OP,OA,如图2,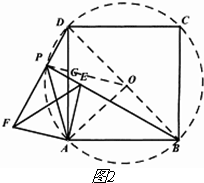
∵∠BAD=∠BPD=90°,
∴OP=OA=$\frac{1}{2}$BD=$\sqrt{2}$,
∴P在以O圆心,$\sqrt{2}$为半径的圆上,
当PA取最大时,PA=OP=OA=$\sqrt{2}$,
点P运动的路径是以O为圆心,以$\sqrt{2}$为半径圆心角是60°的弧的位置,再返回到点A,从另一方向继续以点O为圆心以$\sqrt{2}$为半径旋转60°的弧的位置,再返回,即:4段以点O为圆心,$\sqrt{2}$为半径圆心角是60°的弧的弧长,
∴点P运动的路径长为4×$\frac{\sqrt{2}}{3}$π=$\frac{4\sqrt{2}}{3}$π.
点评 此题是四边形综合题,主要考查了全等三角形的判定和性质,勾股定理,直角三角形的性质,解本题的关键是作出辅助线.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
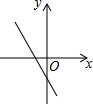
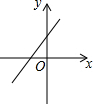
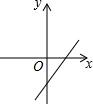
同步拓展阅读系列答案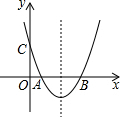 如图,关于x的二次函数y=x2-x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a-1)x+m的图象可能是( )
如图,关于x的二次函数y=x2-x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a-1)x+m的图象可能是( )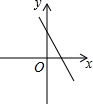
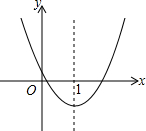 如图,二次函数y=ax2+bx+c的图象如图所示,则下列说法①ac<0;②2a+b<0;③当x=1时,a+b+c>0;④当x=-1时,a-b+c>0;⑤关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.你认为其中正确的有( )
如图,二次函数y=ax2+bx+c的图象如图所示,则下列说法①ac<0;②2a+b<0;③当x=1时,a+b+c>0;④当x=-1时,a-b+c>0;⑤关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.你认为其中正确的有( )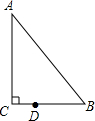 如图,在△ABC中,∠C=90°,∠B=55°,点D在BC边上,DB=2CD,若将△ABC绕点D逆时针旋转α度(0<α<180)后,点B恰好落在初始位置时△ABC的边上,则α等于70或120.
如图,在△ABC中,∠C=90°,∠B=55°,点D在BC边上,DB=2CD,若将△ABC绕点D逆时针旋转α度(0<α<180)后,点B恰好落在初始位置时△ABC的边上,则α等于70或120. 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.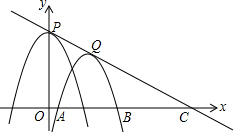 如图,点P是抛物线y=-x2+4的顶点,将抛物线平移,平移后的抛物线与x轴交于A,B两点(A在B的左侧)顶点Q落在第一象限内,且△ABQ是等边三角形,直线PQ与x轴交于点C,若PQ=$\sqrt{3}$,则BC=3$\sqrt{2}$-$\sqrt{3}$.
如图,点P是抛物线y=-x2+4的顶点,将抛物线平移,平移后的抛物线与x轴交于A,B两点(A在B的左侧)顶点Q落在第一象限内,且△ABQ是等边三角形,直线PQ与x轴交于点C,若PQ=$\sqrt{3}$,则BC=3$\sqrt{2}$-$\sqrt{3}$.