题目内容
3.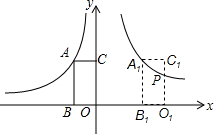 如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上.将矩形向右平移6个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,边C1O1与此图象交于点P,则点P的纵坐标为( )
如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上.将矩形向右平移6个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,边C1O1与此图象交于点P,则点P的纵坐标为( )| A. | $\frac{3}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{2}$ | D. | $\frac{8}{3}$ |
分析 先根据OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上求出AB的长,再由平移的性质得出B1的坐标,进而得出反比例函数的解析式,求出O1的坐标,进而可得出结论.
解答 解:∵OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上,
∴AB=4.
∵将矩形向右平移6个单位长度到A1B1O1C1的位置,
∴(4,0),
∴A1(4,4),
∴k=16,即反比例函数的解析式为y=$\frac{16}{x}$.
∵OB=2,
∴O1(6,0),
∴当x=6时,y=$\frac{16}{6}$=$\frac{8}{3}$,
∴点P的纵坐标为$\frac{8}{3}$.
故选D.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.某地区2015年的交于投入为2.2亿元,计划在未来两年终总共再投入5亿元,设每年教育投入的平均增长率为x,根据题意,可列方程为( )
| A. | 2.2(1+2x)2=5 | B. | 2.2(1+2x)3=5 | ||
| C. | 2.2(1+x)+2.2(1+x2)=5 | D. | 2.2(1+x)+2.2(1+x)3=5 |
14.在-2,π,3,$\sqrt{6}$这四个数中,最大的数是( )
| A. | -2 | B. | π | C. | 3 | D. | $\sqrt{6}$ |
8.下列各组数据中的是三个数作为三角形的边长,其中能构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | C. | 5,6,7 | D. | 7,8,9 |
12.在一个不透明的袋子中,装有5个除数字外其他完全相同的小球,球面上分别写有2、3、4、5、6这5个数字,小苏从袋子中任意摸出一个小球,球面上数字的平方根是无理数的概率是$\frac{4}{5}$.
13.深圳空气质量优良指数排名近年来一直排在全国城市前十.下表是深圳市气象局于2016年3月22日在全市十一个监测点监测到空气质量指数(AQI)数据如表
上述(AQI)数据中,众数和中位数分别是( )
| 监测点 | 荔园 | 西乡 | 华侨城 | 南油 | 盐田 | 龙岗 | 洪湖 | 南澳 | 葵涌 | 梅沙 | 观澜 |
| AQI | 15 | 31 | 25 | 24 | 31 | 24 | 25 | 25 | 34 | 20 | 26 |
| 质量 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 |
| A. | 25,25 | B. | 31,25 | C. | 25,24 | D. | 31,24 |