题目内容
11.已知二次函数y=x2-4x+3.(1)请直接写出此抛物线的顶点坐标及对称轴;
(2)求出此抛物线与两坐标轴的交点坐标.
分析 (1)首先把已知函数解析式配方,然后利用抛物线的顶点坐标、对称轴的公式即可求解;
(2)分别令x=0和y=0即可求出抛物线与两坐标轴的交点坐标.
解答 解:(1)∵y=x2-4x+3=(x-2)2-1,
∴顶点坐标(2,-1),对称轴:直线x=2;
(2)令x=0,得y=3,故与y轴交点为(0,3)
令y=0,得x=1或x=3,故与x轴交点为(1,0),(3,0).
点评 此题主要考查了抛物线与x轴的交点、函数图象的性质及二次函数的三种形式,都是二次函数的基础知识,要求学生熟练掌握.

练习册系列答案
相关题目
19.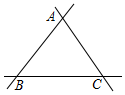 某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建在△ABC的( )
某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建在△ABC的( )
 某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建在△ABC的( )
某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建在△ABC的( )| A. | 两个角的平分线的交点处 | B. | 两边高线的交点处 | ||
| C. | 两边中线的交点处 | D. | 内部即可 |
20.公交车沿东西方向行驶,如果把车站的起点记为0,向东行驶记为正,向西行驶记为负,其中一辆车出发以后行驶的路程如表(单位:km):
(1)该车最后是否回到了车站?为什么?
(2)该车离开出发点最远是多少千米?
(3)这辆车在上述过程中一共行驶了多少路程?
(4)若每行驶1km耗油0.06升,求出该车在上述过程中共耗油多少升?
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
(2)该车离开出发点最远是多少千米?
(3)这辆车在上述过程中一共行驶了多少路程?
(4)若每行驶1km耗油0.06升,求出该车在上述过程中共耗油多少升?
1.在平面直角坐标系中,一条直线经过第三象限内A、B两点,过A、B分别作两坐标轴的垂线与两坐标轴围成的矩形周长均为10,则该直线的函数表达式为( )
| A. | y=x-5 | B. | y=x-10 | C. | y=-x-5 | D. | y=-x-10 |
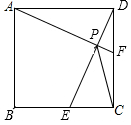 如图,正方形ABCD中,点E为BC的中点,作AF⊥DE交DE、DC分别于P、F点,连PC.
如图,正方形ABCD中,点E为BC的中点,作AF⊥DE交DE、DC分别于P、F点,连PC.

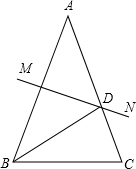 如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,AB=6cm,BC=3cm,则∠DBC=30°,△DBC的周长是9cm.
如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,AB=6cm,BC=3cm,则∠DBC=30°,△DBC的周长是9cm.