题目内容
6.已知数轴上有A、B、C三个点对应的数分别是a、b、c,且满足|a+24|+|b+10|+(c-10)2=0;动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)求a、b、c的值;
(2)若点P到A点距离是到B点距离的2倍,求点P的对应的数;
(3)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后第几秒时,P、Q两点之间的距离为4?请说明理由.
分析 (1)根据绝对值和偶次幂具有非负性可得a+24=0,b+10=0,c-10=0,解可得a、b、c的值;
(2)分两种情况讨论可求点P的对应的数;
(3)分类讨论:当P点在Q点的右侧,且Q点还没追上P点时;当P在Q点左侧时,且Q点追上P点后;当Q点到达C点后,当P点在Q点左侧时;当Q点到达C点后,当P点在Q点右侧时,根据两点间的距离是4,可得方程,根据解方程,可得答案.
解答 解:(1)∵|a+24|+|b+10|+(c-10)2=0,
∴a+24=0,b+10=0,c-10=0,
解得:a=-24,b=-10,c=10;
(2)-10-(-24)=14,
①点P在AB之间,AP=14×$\frac{2}{2+1}$=$\frac{28}{3}$,
-24+$\frac{28}{3}$=-$\frac{44}{3}$,
点P的对应的数是-$\frac{44}{3}$;
②点P在AB的延长线上,AP=14×2=28,
-24+28=4,
点P的对应的数是4;
(3)当P点在Q点的右侧,且Q点还没追上P点时,3t+4=14+t,解得t=5;
当P在Q点左侧时,且Q点追上P点后,3t-4=14+t,解得t=9;
当Q点到达C点后,当P点在Q点左侧时,14+t+4+3t-34=34,t=12.5;
当Q点到达C点后,当P点在Q点右侧时,14+t-4+3t-34=34,解得t=14.5,
综上所述:当Q点开始运动后第5、9、12.5、14.5秒时,P、Q两点之间的距离为4.
点评 此题主要考查了一元一次方程的应用,关键是正确理解题意,掌握非负数的性质,再结合数轴解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.现规定一种新运算“*”:如3*2=32=9,则($\frac{1}{2}$)*3等于( )
| A. | $\frac{1}{6}$ | B. | 8 | C. | $\frac{1}{8}$ | D. | $\frac{3}{2}$ |
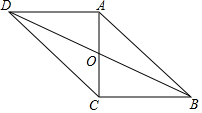 如图,在?ABCD中,对角线AC、BD交于点O,AC⊥BC,且?ABCD的周长为36,△OCD的周长比△OBC的周长大2.
如图,在?ABCD中,对角线AC、BD交于点O,AC⊥BC,且?ABCD的周长为36,△OCD的周长比△OBC的周长大2.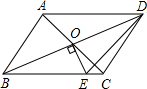 如图,已知?ABCD的对角线交于点O,且AD≠CD,过O作OE⊥BD交BC于E点,若△CDE的周长是8,则?ABCD的周长为16.
如图,已知?ABCD的对角线交于点O,且AD≠CD,过O作OE⊥BD交BC于E点,若△CDE的周长是8,则?ABCD的周长为16. (1)在同一平面直角坐标系中描出下列各点,并将各点用线段依次连接起来:
(1)在同一平面直角坐标系中描出下列各点,并将各点用线段依次连接起来: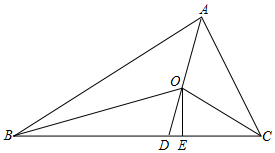 如图,△ABC中,∠ACB>∠ABC,点O是△ABC的内角平分线的交点,AO的延长线交BC于点D,OE⊥BC于点E
如图,△ABC中,∠ACB>∠ABC,点O是△ABC的内角平分线的交点,AO的延长线交BC于点D,OE⊥BC于点E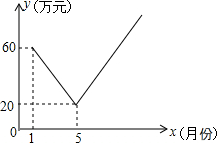 保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2016年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月利润60万元逐月等额下降,到5月份利润为20万元.5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.
保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2016年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月利润60万元逐月等额下降,到5月份利润为20万元.5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.