题目内容
1.判断下列各式是否成立:$\sqrt{2\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$;$\sqrt{3\frac{3}{8}}$=3$\sqrt{\frac{3}{8}}$;$\sqrt{4\frac{4}{15}}$=4$\sqrt{\frac{4}{15}}$;$\sqrt{5\frac{5}{24}}$=5$\sqrt{\frac{5}{24}}$
类比上述式子,再写出两个同类的式子$\sqrt{6\frac{6}{35}}=6\sqrt{\frac{6}{35}}$、$\sqrt{7\frac{7}{48}}=7\sqrt{\frac{7}{48}}$,你能看出其中的规律吗?用字母表示这一规律.
分析 类比上述式子,即可两个同类的式子,然后根据已知的几个式子即可用含n的式子将规律表示出来.
解答 解:$\sqrt{6\frac{6}{35}}=6\sqrt{\frac{6}{35}}$,$\sqrt{7\frac{7}{48}}=7\sqrt{\frac{7}{48}}$,
用字母表示这一规律为:$\sqrt{n+\frac{n}{{n}^{2}-1}}=n\sqrt{\frac{n}{{n}^{2}-1}}$,
故答案为:$\sqrt{6\frac{6}{35}}=6\sqrt{\frac{6}{35}}$,$\sqrt{7\frac{7}{48}}=7\sqrt{\frac{7}{48}}$.
点评 本题主要考查了二次根式的性质与化简,根据式子的特点得到规律,是一个难度适中的题目.

练习册系列答案
相关题目
12.不等式2(1-x)>3的最大整数解是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 无法确定 |
9.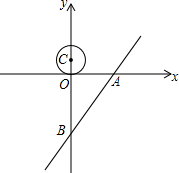 如图所示,直线l的解析式是y=$\frac{4}{3}$x-4,并且与x轴、y轴分别交于A、B点.一个半径为1.5的⊙C,点C坐标为(0,1.5),圆心C以第秒0.5个单位的速度沿着y轴向下运动,当⊙C与直线l相切时,⊙C运动的时间为( )秒.
如图所示,直线l的解析式是y=$\frac{4}{3}$x-4,并且与x轴、y轴分别交于A、B点.一个半径为1.5的⊙C,点C坐标为(0,1.5),圆心C以第秒0.5个单位的速度沿着y轴向下运动,当⊙C与直线l相切时,⊙C运动的时间为( )秒.
 如图所示,直线l的解析式是y=$\frac{4}{3}$x-4,并且与x轴、y轴分别交于A、B点.一个半径为1.5的⊙C,点C坐标为(0,1.5),圆心C以第秒0.5个单位的速度沿着y轴向下运动,当⊙C与直线l相切时,⊙C运动的时间为( )秒.
如图所示,直线l的解析式是y=$\frac{4}{3}$x-4,并且与x轴、y轴分别交于A、B点.一个半径为1.5的⊙C,点C坐标为(0,1.5),圆心C以第秒0.5个单位的速度沿着y轴向下运动,当⊙C与直线l相切时,⊙C运动的时间为( )秒.| A. | 3或6 | B. | 6或10 | C. | 3或16 | D. | 6 或16 |
16.某学习小组8名同学的体重分别是35、50、45、42、36、38、40、42(单位:kg),这组数据的平均数和众数分别为( )
| A. | 41、42 | B. | 41、41 | C. | 36、42 | D. | 36、41 |
6. 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )
 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )| A. | OC∥AE | B. | EC=BC | C. | ∠BOC=2∠CAE | D. | AC⊥OE |
11.下列各图案中,是由一个基本图形通过平移得到的是( )
| A. |  | B. |  | C. |  | D. |  |