题目内容

6．如图，已知AB是⊙O的直径，AD切⊙O于点A，点C是$\widehat{BE}$的中点，则下列结论不成立的是（　　）
A．OC∥AEB．EC=BCC．∠BOC=2∠CAED．AC⊥OE

分析 根据圆周角定理，由AB是⊙O的直径得∠BEA=90°，再根据垂径定理的推理，由点C是$\widehat{BE}$的中点得到OC⊥BE，则可判断OC∥AE，于是可对A选项进行判断；根据垂径定理得$\widehat{BC}$=$\widehat{EC}$，利圆心角、弧、弦的关系可对B选项进行判断；接着可根据圆周角定理对C选项进行判断；由于不能确定$\widehat{CE}$与$\widehat{AE}$相等，则根据垂径定理的推理可对D选项进行判断．

解答 解：∵AB是⊙O的直径，
∴∠BEA=90°，
∴AE⊥BE，
∵点C是$\widehat{BE}$的中点，
∴OC⊥BE，
∴OC∥AE，所以A选项的结论成立；
∴$\widehat{BC}$=$\widehat{EC}$，
∴BC=EC，所以B选项的结论成立；
∠BOC=2∠CAE，所以C选项的结论成立；
∵不能确定$\widehat{CE}$与$\widehat{AE}$相等，
∴不能确定AC⊥OE，所以D选项的结论不成立．
故选D．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了垂径定理和圆周角定理．

练习册系列答案
相关题目
16．已知正比例函数的图象过点（3，-2）和（n，6）．
（1）求正比例函数的表达式；
（2）求n的值．
17．已知线段AB的两个端点的坐标分别为A（2，-1）、B（0，4），若将线段AB向右平移2个单位长度，再向下平移3个单位长度得到线段A′B′，则A′、B′的坐标分别为（4，-4），（2，1）．
14．下面函数中，是正比例函数的是（　　）
A．y=6xB．y=$\frac{-6}{x}$C．y=x2+6xD．y=3x-1
1．判断下列各式是否成立：
$\sqrt{2\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$；$\sqrt{3\frac{3}{8}}$=3$\sqrt{\frac{3}{8}}$；$\sqrt{4\frac{4}{15}}$=4$\sqrt{\frac{4}{15}}$；$\sqrt{5\frac{5}{24}}$=5$\sqrt{\frac{5}{24}}$
类比上述式子，再写出两个同类的式子$\sqrt{6\frac{6}{35}}=6\sqrt{\frac{6}{35}}$、$\sqrt{7\frac{7}{48}}=7\sqrt{\frac{7}{48}}$，你能看出其中的规律吗？用字母表示这一规律．
11．已知一组数据3，a，4，6的众数为3，则这组数据的平均数为（　　）
A．3B．4C．5D．6
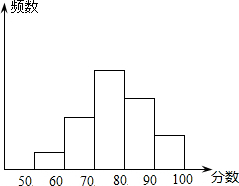18．某班同学参加环保知识竞赛，将学生的成绩（得分取整数）进行整理后分成五组，绘制成频数分布直方图如图，图中从左到右各组的小长方形的高的比为1：3：6：4：2，最后一组的频数为6，结合频数分布直方图提供的信息，回答下列问题：
（1）该班共有多少同学参加竞赛；
（2）成绩落在哪组的数据范围内的人数最多，共有多少人？
（3）求成绩在80分以上（含80分）的学生占全班参赛人数的百分数？
15．把长与宽之比为$\sqrt{2}$的矩形纸片称为标准纸．现有一张标准纸，BC=$\sqrt{2}$，AB=1，将这张标准纸按如图，一次又一次对开后，所得的矩形纸片都是标准纸．问第5次对开后所得标准纸的周长为$\frac{2+\sqrt{2}}{4}$，第2014次对开后所得标准纸的周长为$\frac{1+\sqrt{2}}{{2}^{1006}}$．
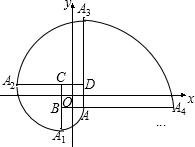16．如图，在直角坐标系中，四边形ABCD是正方形，A（1，-1），B（-1，-1），C（-1，1），D（1，1）．曲线AA1A2A3…叫做“正方形的渐开线”，其中弧AA1、弧A1A2、弧A2A3、弧A3A4…所在圆的圆心依次是点B、C、D、A循环，则点A2015坐标是（1，4031）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网