题目内容
6.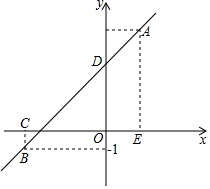 如图,一次函数的图象l经过点A(2,5),B(-4,-1)两点.
如图,一次函数的图象l经过点A(2,5),B(-4,-1)两点.(1)求一次函数表达式.
(2)求直线与x轴的交点C和与y轴的交点D的坐标.
(3)若点E在x轴上,且E(2,0),求△CDE的面积.
(4)你能求出点E到直线l的距离吗?
分析 (1)设一次函数表达式y=kx+b,将A(2,5),B(-4,-1)代入组成方程组,解得k,b可得解析式;
(2)利用(1)的解析式,令y=0可得C点坐标;令x=0可得y的坐标;
(3)连接DE,由三角形的面积公式可得:${S}_{△CDE}=\frac{1}{2}|CE|×$yD;
(4)利用△ACE的面积公式可得点E到直线l的距离.
解答 解:(1)设一次函数表达式y=kx+b,将A(2,5),B(-4,-1)代入组成方程组,
$\left\{\begin{array}{l}{5=2k+b}\\{\;}\\{-1=-4k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{\;}\\{b=3}\end{array}\right.$,
∴一次函数表达式为:y=x+3;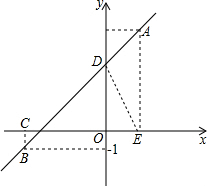
(2)令y=0,则0=x+3,
∴x=-3,
∴C点坐标为(-3,0);
令x=0,y=3;
∴D点坐标为(0,3);
(3)连接DE,${S}_{△CDE}=\frac{1}{2}|CE|×$yD=$\frac{1}{2}×$|2-(-3)|×3=$\frac{15}{2}$;
(4)∵△ACE的面积为:$\frac{1}{2}×5×$5=$\frac{25}{2}$;
|AC|=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$,
∴点E到直线l的距离为:$\frac{25}{2}÷\frac{1}{2}÷5\sqrt{2}$=$\frac{5\sqrt{2}}{2}$.
点评 本题主要考查了待定系数法求一次函数的解析式及一次函数图象上点的坐标特征,利用面积法求得点到直线的距离是解答此题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
7.下列运算正确的有( )
| A. | 5ab-ab=4 | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | a6÷a3=a3 | D. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{2}{a+b}$ |
1.用配方法解一元二次方程2x2-4x+1=0,变形正确的是( )
| A. | (x-$\frac{1}{2}$)2=0 | B. | (x-$\frac{1}{2}$)2=$\frac{1}{2}$ | C. | (x-1)2=$\frac{1}{2}$ | D. | (x-1)2=0 |
18.经过点(0,-2),且与直线y=3x平行的直线是( )
| A. | y=3x+2 | B. | y=3x-2 | C. | y=-3x+2 | D. | y=-3x-2 |
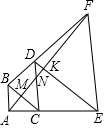 如图,以等腰直角△ABC的斜边BC为直角边向外作第二个等腰直角△BCD,再以等腰直角△BCD的斜边CD为直角边向外作第三个等腰直角△CDE,再以等腰直角△CDE的斜边DE为直角边向外作第四个等腰直角△DEF.连结AF分别交BC,DC,DE于点M,N,K,若S△ABM+S△DNK=13,则△CMN的面积为16.
如图,以等腰直角△ABC的斜边BC为直角边向外作第二个等腰直角△BCD,再以等腰直角△BCD的斜边CD为直角边向外作第三个等腰直角△CDE,再以等腰直角△CDE的斜边DE为直角边向外作第四个等腰直角△DEF.连结AF分别交BC,DC,DE于点M,N,K,若S△ABM+S△DNK=13,则△CMN的面积为16.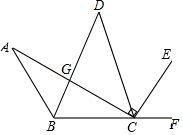 如图,AB∥CD,BD平分∠ABC,∠ACE=90°,AC⊥BD
如图,AB∥CD,BD平分∠ABC,∠ACE=90°,AC⊥BD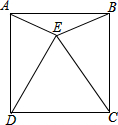 如图,E为正方形ABCD内的一点,且△DCE为等边三角形,则∠CBE=75°,∠ABE=15°.
如图,E为正方形ABCD内的一点,且△DCE为等边三角形,则∠CBE=75°,∠ABE=15°.