题目内容
11.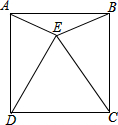 如图,E为正方形ABCD内的一点,且△DCE为等边三角形,则∠CBE=75°,∠ABE=15°.
如图,E为正方形ABCD内的一点,且△DCE为等边三角形,则∠CBE=75°,∠ABE=15°.
分析 由E为正方形ABCD内一点,且△EDC是等边三角形,易证得△BCE是等腰三角形,易求得∠BCE=30°,继而根据三角形内角和求得答案.
解答 解:∵E为正方形ABCD内一点,且△EDC是等边三角形,
∴∠DCB=90°,∠ECD=60°,BC=CD=EC,
∴∠BCE=∠BCD-∠ECD=30°,
∴∠EBC=∠BEC=$\frac{1}{2}$(180°-30°)=75°,
∴∠ABE=90°-75°=15°.
故答案为:75°,15°.
点评 此题考查了正方形的性质以及等边三角形的性质.解题时注意:正方形的四条边都相等,四个角都是直角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.对于函数y=-$\frac{3}{x}$,当x<0时,函数图象位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
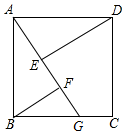 在边长为4cm的正方形ABCD中,点G是射线CB上的一点,E、F为直线AG上两个动点,连接DE、BF.
在边长为4cm的正方形ABCD中,点G是射线CB上的一点,E、F为直线AG上两个动点,连接DE、BF.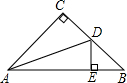 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB交AB于点E,AB=4$\sqrt{2}$cm,求△BDE的周长.
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB交AB于点E,AB=4$\sqrt{2}$cm,求△BDE的周长.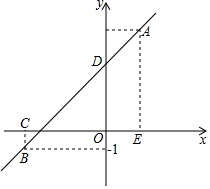 如图,一次函数的图象l经过点A(2,5),B(-4,-1)两点.
如图,一次函数的图象l经过点A(2,5),B(-4,-1)两点.