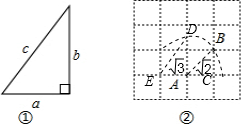题目内容
1. 如图,在△ABC中,∠B=∠C=30°,D在BC上,CD=2BD,求证:AD=BD.
如图,在△ABC中,∠B=∠C=30°,D在BC上,CD=2BD,求证:AD=BD.
分析 作AE⊥BC,设BD=x,则CD=2x.根据勾股定理计算出AD的长,即可知道BD=AD.
解答  解:作AE⊥BC,
解:作AE⊥BC,
设BD=x,则CD=2x.
又∵∠B=∠C=30°,
∴BE=$\frac{1}{2}$×3x=$\frac{3x}{2}$,
在Rt△ABE中,AE=$\frac{3x}{2}$•tan30°=$\frac{3x}{2}$•$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{2}$x,
在Rt△ADE中,
AD=$\sqrt{{(\frac{1}{2}x)}^{2}+{(\frac{\sqrt{3}}{2}x)}^{2}}$=x,
∴BD=AD.
点评 本题考查了勾股定理,作出辅助线,求出AD的长即可知道BD=AD.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
11. 如图,阴影部分在长为a,宽为b的长方形中,当a=10,b=6时,阴影部分的面积是( )
如图,阴影部分在长为a,宽为b的长方形中,当a=10,b=6时,阴影部分的面积是( )
 如图,阴影部分在长为a,宽为b的长方形中,当a=10,b=6时,阴影部分的面积是( )
如图,阴影部分在长为a,宽为b的长方形中,当a=10,b=6时,阴影部分的面积是( )| A. | 8 | B. | 15 | C. | 30 | D. | 60 |
9. 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )
 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )| A. | 3 | B. | $\frac{20}{3}$ | C. | 1 | D. | $\frac{16}{3}$ |
6.在⊙O内有一点P,已知OP=$\sqrt{3}$,且圆内过点P的最短弦长为6,则⊙O的面积是( )
| A. | 6π | B. | 8π | C. | 10π | D. | 12π |
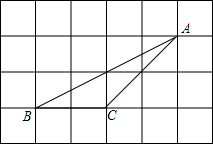 如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于$\frac{1}{3}$.
如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于$\frac{1}{3}$.