题目内容
12.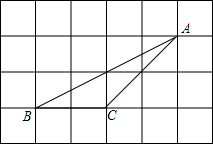 如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于$\frac{1}{3}$.
如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于$\frac{1}{3}$.
分析 设小正方形的边长为1,过C作CF⊥AB于F,根据勾股定理求出AB、AC,根据三角形面积公式求出CF,根据勾股定理求出AF,解直角三角形求出即可.
解答 解: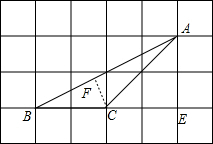
设小正方形的边长为1,
过C作CF⊥AB于F,
由勾股定理得:AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,AC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,BC=2,
由三角形面积公式得:AB×CF=BC×AE,
2$\sqrt{5}$×CF=2×2,
解得:CF=$\frac{2\sqrt{5}}{5}$,
在Rt△AFC中,由勾股定理得:AF=$\sqrt{A{C}^{2}-C{F}^{2}}$=$\frac{6\sqrt{5}}{5}$
tan∠BAC=$\frac{CF}{AF}$=$\frac{\frac{2\sqrt{5}}{5}}{\frac{6\sqrt{5}}{5}}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查了解直角三角形,勾股定理的应用,解此题的关键是构造直角三角形,难度适中.

练习册系列答案
相关题目
20.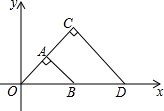 如图,等腰Rt△OAB和等腰Rt△OCD中,∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,若点B的坐标为(1,0),则点C的坐标为( )
如图,等腰Rt△OAB和等腰Rt△OCD中,∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,若点B的坐标为(1,0),则点C的坐标为( )
 如图,等腰Rt△OAB和等腰Rt△OCD中,∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,若点B的坐标为(1,0),则点C的坐标为( )
如图,等腰Rt△OAB和等腰Rt△OCD中,∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,若点B的坐标为(1,0),则点C的坐标为( )| A. | (1,1) | B. | (2,2) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | ($\frac{3}{2}$,$\frac{3}{2}$) |
7.某种衬衣的价格经过连续两次降价后,由每件150元降至96元,平均每次降价的百分率是( )
| A. | 10% | B. | 20% | C. | 30% | D. | 40% |
17.某中学排球队12名队员的年龄情况如下表:
则这个队员年龄的众数是14.
| 年龄(岁) | 12 | 13 | 14 | 15 |
| 人数(人) | 1 | 2 | 5 | 4 |
 如图,在△ABC中,∠B=∠C=30°,D在BC上,CD=2BD,求证:AD=BD.
如图,在△ABC中,∠B=∠C=30°,D在BC上,CD=2BD,求证:AD=BD.