题目内容
9. 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )| A. | 3 | B. | $\frac{20}{3}$ | C. | 1 | D. | $\frac{16}{3}$ |
分析 由以△ABC的边AB为直径的半圆O,根据直径所对的圆周角是直角,可求得∠ACB=90°又由CD⊥AB,根据同角的余角相等,易证得∠B=∠ACD,又由cos∠ACD=$\frac{3}{5}$,BC=5,即可求得答案.
解答 解:∵AB为直径,
∴∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD⊥AB,
∴∠B+∠BCD=90°,
∴∠B=∠ACD,
∵cos∠ACD=$\frac{3}{5}$,
∴tan∠ACD=tan∠B=$\frac{4}{3}$,
∵BC=5,
∴AC=BC•tan∠B=$\frac{20}{3}$.
故选B.
点评 此题考查了圆周角定理.注意证得∠ACD=∠B是关键.

练习册系列答案
相关题目
20.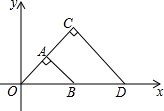 如图,等腰Rt△OAB和等腰Rt△OCD中,∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,若点B的坐标为(1,0),则点C的坐标为( )
如图,等腰Rt△OAB和等腰Rt△OCD中,∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,若点B的坐标为(1,0),则点C的坐标为( )
 如图,等腰Rt△OAB和等腰Rt△OCD中,∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,若点B的坐标为(1,0),则点C的坐标为( )
如图,等腰Rt△OAB和等腰Rt△OCD中,∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,若点B的坐标为(1,0),则点C的坐标为( )| A. | (1,1) | B. | (2,2) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | ($\frac{3}{2}$,$\frac{3}{2}$) |
17.某中学排球队12名队员的年龄情况如下表:
则这个队员年龄的众数是14.
| 年龄(岁) | 12 | 13 | 14 | 15 |
| 人数(人) | 1 | 2 | 5 | 4 |
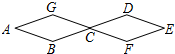 如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由点A开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2014厘米后停下,则这只蚂蚁停在( )
如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由点A开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2014厘米后停下,则这只蚂蚁停在( ) 如图,在△ABC中,∠B=∠C=30°,D在BC上,CD=2BD,求证:AD=BD.
如图,在△ABC中,∠B=∠C=30°,D在BC上,CD=2BD,求证:AD=BD.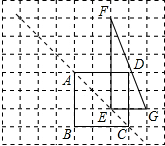 如图,方格纸中每个小正方形的边长均为1,正方形ABCD和△EFG的顶点都在小正方形的顶点上.
如图,方格纸中每个小正方形的边长均为1,正方形ABCD和△EFG的顶点都在小正方形的顶点上.