题目内容
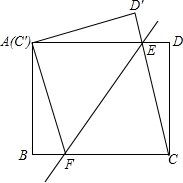 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,BC于点F,连接AF、CE.
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,BC于点F,连接AF、CE.(1)求证:△AFE为等腰三角形.
(2)设AE=a,ED=b,DC=c.请写出一个a,b,c三者之间的数量关系式.
(3)若AB=12cm,BC=18cm,求重叠部分△AFE的面积和EF的长.
考点:翻折变换(折叠问题)
专题:
分析:(1)证明∠AFE=∠AEF,即可解决问题.
(2)证明AE=CF,运用勾股定理即可解决问题.
(3)证明四边形AFCE是菱形,求出AC、AE的长度,即可解决问题.
(2)证明AE=CF,运用勾股定理即可解决问题.
(3)证明四边形AFCE是菱形,求出AC、AE的长度,即可解决问题.
解答: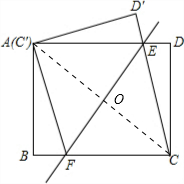 解:(1)如图,连接AC,交EF于点O;
解:(1)如图,连接AC,交EF于点O;
由题意得:∠AFE=∠CFE;
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠AEF=∠CFE,
∴∠AFE=∠AEF,
∴AE=AF,
∴△AFE为等腰三角形.
(2)∵EF⊥AC,且平分AC,
∴AE=CE=a;在Rt△DCE中,
由勾股定理得:
CE2=CD2+DE2,而ED=b,DC=c,
∴a2=b2+c2.
(3)∵四边形ABCD为矩形,
∴∠B=90°,
∴AC2=BC2+AB2=122+182,
∴AC=6
;
由矩形的中心对称性知:AE=CF,而AE∥CF,
∴四边形AFCE是平行四边形,而AE=AF,
∴四边形AFCE是菱形,AC⊥EF;
设AE=λ,则DE=18-λ;
由(2)知:λ2=(18-λ)2+122,
解得:λ=13,
∴S菱形AECF=AE•CD=
AC•EF=13×12,
∴S△AEF=
S菱形AECF=78,EF=
,
即重叠部分△AFE的面积和EF的长分别为78cm2、
cm.
 解:(1)如图,连接AC,交EF于点O;
解:(1)如图,连接AC,交EF于点O;由题意得:∠AFE=∠CFE;
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠AEF=∠CFE,
∴∠AFE=∠AEF,
∴AE=AF,
∴△AFE为等腰三角形.
(2)∵EF⊥AC,且平分AC,
∴AE=CE=a;在Rt△DCE中,
由勾股定理得:
CE2=CD2+DE2,而ED=b,DC=c,
∴a2=b2+c2.
(3)∵四边形ABCD为矩形,
∴∠B=90°,
∴AC2=BC2+AB2=122+182,
∴AC=6
| 13 |
由矩形的中心对称性知:AE=CF,而AE∥CF,
∴四边形AFCE是平行四边形,而AE=AF,
∴四边形AFCE是菱形,AC⊥EF;
设AE=λ,则DE=18-λ;
由(2)知:λ2=(18-λ)2+122,
解得:λ=13,
∴S菱形AECF=AE•CD=
| 1 |
| 2 |
∴S△AEF=
| 1 |
| 2 |
52
| ||
| 3 |
即重叠部分△AFE的面积和EF的长分别为78cm2、
52
| ||
| 3 |
点评:该题以矩形为载体,以翻折变换为方法,以等腰三角形的判定、勾股定理、菱形的判定及其性质等几何知识点的考查为核心构造而成;解题的关键是作辅助线;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
A和B都是6次多项式,则A+B一定是( )
| A、6次多项式 |
| B、12次多项式 |
| C、次数不低于6的多项式 |
| D、次数不高于6的多项式或单项式 |
下面说法正确的有( )
(1)正整数和负整数统称有理数;(2)0既不是正数,又不是负数;(3)0表示没有;(4)正数和负数统称有理数.
(1)正整数和负整数统称有理数;(2)0既不是正数,又不是负数;(3)0表示没有;(4)正数和负数统称有理数.
| A、4个 | B、3个 | C、2个 | D、1个 |
 若每个小正方形边长为1分米,共摆放了8层,现要将靠墙及地面的部分涂上防锈漆,求防锈漆的总面积.
若每个小正方形边长为1分米,共摆放了8层,现要将靠墙及地面的部分涂上防锈漆,求防锈漆的总面积. 小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)
小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)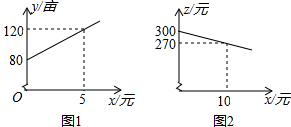 某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系. 如图,在△ABC中,EF∥DC,∠AFE=∠B,AE=6,DE=3,AF=8.
如图,在△ABC中,EF∥DC,∠AFE=∠B,AE=6,DE=3,AF=8.