题目内容
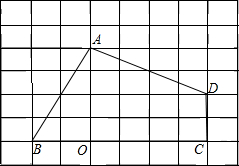如图，在8×6正方形网格图中，每个小正方形边长均为1，点O和四边形ABCD的顶点均在小正方形的顶点上．（1）以O为位似中心，在网格图中作四边形A′B′C′D′和四边形ABCD位似，且位似比为1：2；
（2）根据（1）填空：
①OD′：D′D=
②
| S四边形OA‘D’C‘ |
| S四边形OADC |
考点：作图-位似变换
专题：网格型
分析：（1）利用位似图形的性质得出对应点位置进而得出答案；
（2）①②利用位似比得出相似比，再利用相似图形的性质得出即可．
（2）①②利用位似比得出相似比，再利用相似图形的性质得出即可．
解答：
解：（1）如图所示：四边形A′B′C′D′即为所求；
（2）①∵四边形A′B′C′D′和四边形ABCD位似，且位似比为1：2，
∴OD′：D′D=1：1；
故答案为：1：1；
②∵四边形A′B′C′D′和四边形ABCD位似，且位似比为1：2，
∴
=
．
故答案为：
．
解：（1）如图所示：四边形A′B′C′D′即为所求；（2）①∵四边形A′B′C′D′和四边形ABCD位似，且位似比为1：2，
∴OD′：D′D=1：1；
故答案为：1：1；
②∵四边形A′B′C′D′和四边形ABCD位似，且位似比为1：2，
∴
| S四边形OA‘D’C‘ |
| S四边形OADC |
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：此题主要考查了位似变换的性质，得出对应点位置是解题关键．
练习册系列答案
相关题目
若每个小正方形边长为1分米，共摆放了8层，现要将靠墙及地面的部分涂上防锈漆，求防锈漆的总面积．
如图，在△ABC中，EF∥DC，∠AFE=∠B，AE=6，DE=3，AF=8．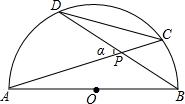
如图，C、D是以AB为直径的半圆上的两个点（不与A、B重合），连接DC、AC、DB，AC与BD交于点P，若∠APD=α，则
下面说法正确的有（ ）
（1）正整数和负整数统称有理数；（2）0既不是正数，又不是负数；（3）0表示没有；（4）正数和负数统称有理数．
（1）正整数和负整数统称有理数；（2）0既不是正数，又不是负数；（3）0表示没有；（4）正数和负数统称有理数．
| A、4个 | B、3个 | C、2个 | D、1个 |
如图，是用七巧板拼成一个图形，其中③、⑥、①板的面积分别为S③，S⑥，S①，则 S③：S⑥：S①=
作图题（要求：尺规作图，写出作法并保留作图痕迹）