题目内容
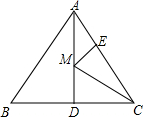 如图,等边△ABC的边长为6,面积为9
如图,等边△ABC的边长为6,面积为9| 3 |
考点:轴对称-最短路线问题,等边三角形的性质
专题:
分析:要求EM+CM的最小值,需考虑通过作辅助线转化EM,CM的值,从而找出其最小值求解.
解答: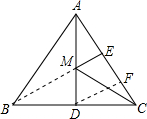 解:连接BE,与AD交于点M.
解:连接BE,与AD交于点M.
∵AD是BC边上的中线,
∴AD⊥BC,
∴AD是BC的垂直平分线,
∴B、C关于AD对称,
∴BE就是EM+CM的最小值.
取CE中点F,连接DF.
∵等边△ABC的边长为6,面积为9
,
∴AD=3
∵AE=2,
∴CE=AC-AE=6-2=4,
∴CF=EF=AE=2,
又∵AD是BC边上的中线,
∴DF是△BCE的中位线,
∴BE=2DF,BE∥DF,
又∵E为AF的中点,
∴M为AD的中点,
∴ME是△ADF的中位线,
∴DF=2ME,
∴BE=2DF=4ME,
∴BM=BE-ME=4ME-ME=3ME,
∴BE=
BM.
在直角△BDM中,BD=
BC=3,DM=
AD=
,
∴BM=
=
,
∴BE=
BM=2
.
∵EM+CM=BE
∴EM+CM的最小值为2
.
故答案为2
.
 解:连接BE,与AD交于点M.
解:连接BE,与AD交于点M.∵AD是BC边上的中线,
∴AD⊥BC,
∴AD是BC的垂直平分线,
∴B、C关于AD对称,
∴BE就是EM+CM的最小值.
取CE中点F,连接DF.
∵等边△ABC的边长为6,面积为9
| 3 |
∴AD=3
| 3 |
∵AE=2,
∴CE=AC-AE=6-2=4,
∴CF=EF=AE=2,
又∵AD是BC边上的中线,
∴DF是△BCE的中位线,
∴BE=2DF,BE∥DF,
又∵E为AF的中点,
∴M为AD的中点,
∴ME是△ADF的中位线,
∴DF=2ME,
∴BE=2DF=4ME,
∴BM=BE-ME=4ME-ME=3ME,
∴BE=
| 4 |
| 3 |
在直角△BDM中,BD=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
∴BM=
| BD2+DM2 |
| 3 |
| 2 |
| 7 |
∴BE=
| 4 |
| 3 |
| 7 |
∵EM+CM=BE
∴EM+CM的最小值为2
| 7 |
故答案为2
| 7 |
点评:考查等边三角形的性质和轴对称及勾股定理等知识的综合应用,熟练掌握和运用等边三角形的性质以及轴对称的性质是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
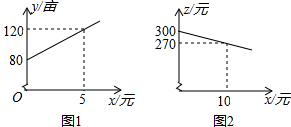 某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系. 如图,在△ABC中,EF∥DC,∠AFE=∠B,AE=6,DE=3,AF=8.
如图,在△ABC中,EF∥DC,∠AFE=∠B,AE=6,DE=3,AF=8. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论: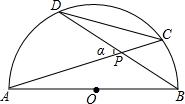 如图,C、D是以AB为直径的半圆上的两个点(不与A、B重合),连接DC、AC、DB,AC与BD交于点P,若∠APD=α,则
如图,C、D是以AB为直径的半圆上的两个点(不与A、B重合),连接DC、AC、DB,AC与BD交于点P,若∠APD=α,则