Question

3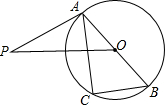．如图，已知AB是⊙O的直径，OP垂直于弦AC，PA是⊙O的切线，求证：△ABC∽△POA．

Answer 1

分析 根据直径所对的圆周角为直角可知∠C=90°，又OP垂直于弦AC，可得BC∥OP，根据平行线的性质得出∠B=∠AOP，再根据切线的性质知∠OAP=90°，利用有两组角对应相等的两个三角形相似，即可证明△ABC∽△POA．

解答 证明：∵AB是直径，
∴∠C=90°，即BC⊥AC，
∵OP⊥AC，
∵BC∥OP，
∴∠B=∠AOP，
∵PA是⊙O的切线，切点为A，
∴∠OAP=90°，
∴∠C=∠OAP，
∴△ABC∽△POA．

点评 本题考查了相似三角形的判定，切线的性质，平行线的性质等知识，掌握相似三角形的判定定理是解题的关键．