题目内容
14. 在一条笔直的公路的同侧依次排列着A,C,B三个村庄,某天甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止,从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.
在一条笔直的公路的同侧依次排列着A,C,B三个村庄,某天甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止,从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.求:(1)甲的速度是60km/h,乙的速度是80km/h;
(2)分别求出甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系式,并写出取值范围;
(3)若甲、乙两车到C地后继续沿该公路原速度行驶,求甲车出发多少小时,两车相距350km.
分析 (1)根据速度=路程÷时间即可算出甲、乙两车的速度;
(2)根据y甲=240-速度×时间即可列出y甲关于t的函数关系式;当0≤t≤1时,y乙=240;当1≤t≤4时,根据y乙=240-速度×时间即可列出y乙关于t的函数关系式;
(3)当两车经过C地继续行驶时,先分析二者相距350km时,乙车有没有到达A地,再根据时间=路程÷速度和+4即可求出二者相距350km的时间.
解答 解:(1)240÷4=60(km/h);
240÷(4-1)=80(km/h).
故答案为:60km/h;80km/h.
(2)根据题意得:y甲=-60t+240(0≤t≤4).
当0≤t≤1时,y乙=240;
当1≤t≤4时,y乙=240-80(t-1)=-80t+320.
∴y乙=$\left\{\begin{array}{l}{240(0≤t≤1)}\\{-80t+320(1≤t≤4)}\end{array}\right.$.
(3)当甲、乙两车经过C地继续行驶时,350÷(80+60)=$\frac{5}{2}$(h),
∵80×$\frac{5}{2}$=200(km),200<240,
∴当甲、乙两车离开C地并相距350km时,乙车尚未到达A地,
∴$\frac{5}{2}$+4=$\frac{13}{2}$(h).
答:甲车出发$\frac{13}{2}$h时,两车相距350km.
点评 本题考查了一次函数的应用以及解一元一次方程,解题的关键是:(1)根据速度=路程÷时间列式计算;(2)根据y=240-速度×时间列出y甲、y乙关于t的函数关系式;(3)根据时间=路程÷速度和+4列式计算.

练习册系列答案
相关题目

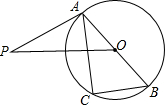 如图,已知AB是⊙O的直径,OP垂直于弦AC,PA是⊙O的切线,求证:△ABC∽△POA.
如图,已知AB是⊙O的直径,OP垂直于弦AC,PA是⊙O的切线,求证:△ABC∽△POA.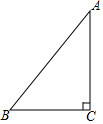 如图,已知Rt△ABC,∠C=90°,AC≠BC.
如图,已知Rt△ABC,∠C=90°,AC≠BC.