题目内容
11. 如图,在平面直角坐标系中,O为坐标原点,抛物线F:y=ax2+2ax+c经过A(-4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.
如图,在平面直角坐标系中,O为坐标原点,抛物线F:y=ax2+2ax+c经过A(-4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.(1)求抛物线的解析式及顶点坐标;
(2)求点B关于直线y=x+5的对称点B′,并判断点B′是否在抛物线的对称轴上;
(3)画出函数y=|ax2+2ax+c|的图象F′,并写出过点B且与图象F′恰有三个公共点的直线表达式.
分析 (1)利用待定系数法即可解决问题.
(2)如图1中,连接BB′交DE于K.求出B′的坐标即可解决问题.
(3)如图2中,当直线y=kx+4与抛物线y=-$\frac{1}{2}$x2-x+4只有一个交点时,过点B且与图象F′恰有三个公共点,把问题转化为方程组$\left\{\begin{array}{l}{y=kx+4}\\{y=-\frac{1}{2}{x}^{2}-x+4}\end{array}\right.$只有一组解即可解决问题.
解答 解:(1)把A(-4,0),B(0,4)两点坐标代入y=ax2+2ax+c得到$\left\{\begin{array}{l}{c=4}\\{16a-8a+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=4}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2-x+4.
∵y=-$\frac{1}{2}$x2-x+4=-$\frac{1}{2}$(x+1)2+$\frac{9}{2}$,
∴顶点坐标为(-1,$\frac{9}{2}$).
(2)如图1中,连接BB′交DE于K.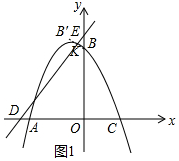
∵直线DE的解析式为y=x+5,BB′⊥DE,
∴直线BB′的解析式为y=-x+4,
由$\left\{\begin{array}{l}{y=-x+4}\\{y=x+5}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{9}{2}}\end{array}\right.$,
∴K(-$\frac{1}{2}$,$\frac{9}{2}$),
∵BK=KB′,
∴B′(-1,5),
∵抛物线的对称轴x=-1,
∴点B′在抛物线的对称轴上.
(3)如图2中,当直线y=kx+4与抛物线y=-$\frac{1}{2}$x2-x+4只有一个交点时,过点B且与图象F′恰有三个公共点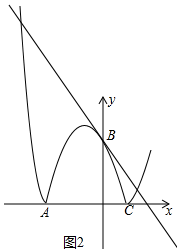
由$\left\{\begin{array}{l}{y=kx+4}\\{y=-\frac{1}{2}{x}^{2}-x+4}\end{array}\right.$消去y得到x2+(2+2k)x=0,
由题意△=0,∴2+2k=0,
∴k=-1,
∴过点B且与图象F′恰有三个公共点的直线表达式为y=-x+4.
点评 本题考查二次函数与坐标轴的交点、一次函数的应用、一元二次方程的根的判别式等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案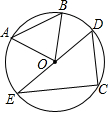 如图,已知AB,CD是⊙O的弦,且AB=CD,∠AOB=70°,则∠CED的度数为( )
如图,已知AB,CD是⊙O的弦,且AB=CD,∠AOB=70°,则∠CED的度数为( )| A. | 70° | B. | 60° | C. | 45° | D. | 35° |

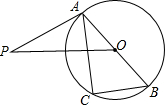 如图,已知AB是⊙O的直径,OP垂直于弦AC,PA是⊙O的切线,求证:△ABC∽△POA.
如图,已知AB是⊙O的直径,OP垂直于弦AC,PA是⊙O的切线,求证:△ABC∽△POA. 如图,已知一次函数y=x-2与反比例函数y=$\frac{3}{x}$的图象交于A、B两点.
如图,已知一次函数y=x-2与反比例函数y=$\frac{3}{x}$的图象交于A、B两点. 如图,在小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据图形解答下列问题:
如图,在小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据图形解答下列问题: