题目内容
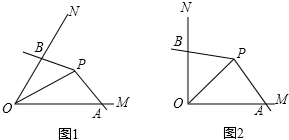
16.一艘轮船以12海里/小时的速度离开A港向北偏西30°方向航行,另一艘轮船以16海里/小时的速度离开A港北偏东60°方向航行,经过1.5小时后他们相距30海里.分析 根据方向角的概念画出图形,再利用勾股定理解答.
解答 解:如图:
∵∠BAD=30°,∠DAC=60°,
∴∠BAC=90°,
∵设AB=12×1.5=18海里,AC=16×1.5=24海里,
根据勾股定理得,BC=$\sqrt{1{8}^{2}+2{4}^{2}}$=30海里.
故答案为:30.
点评 本题考查了勾股定理的应用,熟悉方向角和勾股定理及二次根式的运算是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在-$\frac{π}{3}$,$\sqrt{16}$,$\frac{\sqrt{2}}{2}$,0.3030030003,-$\frac{22}{7}$,3.14中,有理数有几个( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1.点A(m-3,m+1)在第二、四象限的平分线上,则A的坐标为( )
| A. | (-1,1) | B. | (-2,-2) | C. | (-2,2) | D. | (2,2) |
5.下列命题是真命题的是( )
| A. | 直角三角形中两个锐角互补 | B. | 相等的角是对顶角 | ||
| C. | 同旁内角互补,两直线平行 | D. | 若|a|=|b|,则a=b |
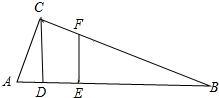 如图,已知在△ABC中,∠ACB=90°,CD是斜边AB上的高,在AB上截取AE=AC,过点E作EF∥CD,交BC于点F,DE=1厘米,求点E到BC的距离.
如图,已知在△ABC中,∠ACB=90°,CD是斜边AB上的高,在AB上截取AE=AC,过点E作EF∥CD,交BC于点F,DE=1厘米,求点E到BC的距离.