题目内容
3.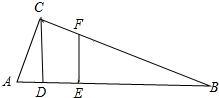 如图,已知在△ABC中,∠ACB=90°,CD是斜边AB上的高,在AB上截取AE=AC,过点E作EF∥CD,交BC于点F,DE=1厘米,求点E到BC的距离.
如图,已知在△ABC中,∠ACB=90°,CD是斜边AB上的高,在AB上截取AE=AC,过点E作EF∥CD,交BC于点F,DE=1厘米,求点E到BC的距离.
分析 连接CE,作EG⊥BC于G,根据等边对等角得出∠ACE=∠AEC,因为∠AEC+∠DCE=90°,∠ACE+∠ECF=∠ACB=90°,得出CE是∠DCF的角平分线,根据角平分线的性质即可证得EG=DE=1厘米,即可得出点E到BC的距离.
解答 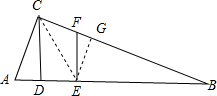 解:连接CE,作EG⊥BC于G,
解:连接CE,作EG⊥BC于G,
∵AE=AC,
∴∠ACE=∠AEC,
∵CD⊥AB,
∴∠AEC+∠DCE=90°,
∵∠ACE+∠ECF=∠ACB=90°,
∴∠DCE=∠GCE,
∵DE⊥CD,EG⊥BC,
∴EG=DE=1.
∴点E到BC的距离为1厘米.
点评 本题考查了等腰三角形的性质,角平分线的性质,作出辅助线证得CE是角平分线是解题的关键.

练习册系列答案
相关题目
13.2008年5月12日,四川汶川发生8.3级大地震,据统计这次地震直接经济损失大约600 000 000 000元,这个数据用科学记数法表示为( )
| A. | 0.6×1012元 | B. | 6×1012元 | C. | 6×1011元 | D. | 60×1010元 |
14.下列各组数据不能作为直角三角形的三边长的是( )
| A. | a=3 b=4 c=5 | B. | a=6 b=8 c=10 | C. | a=5 b=12 c=13 | D. | a=13 b=16 c=18 |
15. 如图在△ABD和△ACE都是等边三角形,则△ADC≌△ABE的根据是( )
如图在△ABD和△ACE都是等边三角形,则△ADC≌△ABE的根据是( )
 如图在△ABD和△ACE都是等边三角形,则△ADC≌△ABE的根据是( )
如图在△ABD和△ACE都是等边三角形,则△ADC≌△ABE的根据是( )| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
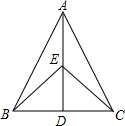 已知:如图,AB=AC,AD⊥BC于D,点E在AD上,图中共有3对全等三角形.
已知:如图,AB=AC,AD⊥BC于D,点E在AD上,图中共有3对全等三角形.
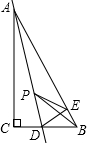 如图所示,在Rt△ABC中,∠C=90°,∠ABC=60°,点D是BC边上的点,BD=2,将△ABC沿直线AD翻折,使点C落在AB边上的点E处.若点P是直线AD上的动点,则△PEB的周长的最小值是3+$\sqrt{3}$.
如图所示,在Rt△ABC中,∠C=90°,∠ABC=60°,点D是BC边上的点,BD=2,将△ABC沿直线AD翻折,使点C落在AB边上的点E处.若点P是直线AD上的动点,则△PEB的周长的最小值是3+$\sqrt{3}$. 已知一次函数y=kx+b的图象经过点A(-1,-5),且与正比例函数y=$\frac{1}{2}x$的图象相交于点B(2,a).
已知一次函数y=kx+b的图象经过点A(-1,-5),且与正比例函数y=$\frac{1}{2}x$的图象相交于点B(2,a).