题目内容
15. 如图,一个正方形内两个相邻正方形的面积分别为4和2,它们都有两个顶点在大正方形的边上且组成的图形为轴对称图形,则图中阴影部分的面积为$\frac{3}{4}$+$\frac{9\sqrt{2}}{2}$.
如图,一个正方形内两个相邻正方形的面积分别为4和2,它们都有两个顶点在大正方形的边上且组成的图形为轴对称图形,则图中阴影部分的面积为$\frac{3}{4}$+$\frac{9\sqrt{2}}{2}$.
分析 连接AC;由正方形的性质和已知条件得出EF=$\sqrt{2}$,GH=2,∠EAF=∠GCH=90°,由轴对称图形的性质得出AE=AF,CG=CH,得出AM=$\frac{1}{2}$EF=$\frac{\sqrt{2}}{2}$,CN=$\frac{1}{2}$GH=1,求出AC的长,得出正方形ABCD的面积,由大正方形的面积减去两个小正方形的面积即可得出图中阴影部分的面积.
解答 解:如图所示:连接AC;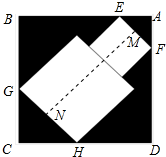 ∵正方形ABCD内两个相邻正方形的面积分别为4和2,
∵正方形ABCD内两个相邻正方形的面积分别为4和2,
∴EF=$\sqrt{2}$,GH=2,∠EAF=∠GCH=90°,
根据题意得:AE=AF,CG=CH,
∴AM=$\frac{1}{2}$EF=$\frac{\sqrt{2}}{2}$,CN=$\frac{1}{2}$GH=1,
∴AC=$\frac{\sqrt{2}}{2}$+$\sqrt{2}$+2+1=$\frac{3\sqrt{2}}{2}$+3,
∴正方形ABCD的面积=$\frac{1}{2}$AC2=$\frac{1}{2}$($\frac{3\sqrt{2}}{2}$+3)2=$\frac{27}{4}$+$\frac{9\sqrt{2}}{2}$,
∴图中阴影部分的面积=$\frac{27}{4}$+$\frac{9\sqrt{2}}{2}$-4-2=$\frac{3}{4}$+$\frac{9\sqrt{2}}{2}$;
故答案为:$\frac{3}{4}$+$\frac{9\sqrt{2}}{2}$.
点评 本题考查了正方形的性质、轴对称图形的性质、等腰直角三角形的性质、正方形面积的计算方法;熟练掌握正方形的性质,通过作辅助线求出对角线AC是解决问题的关键.

练习册系列答案
相关题目
6.一学生扔实心球,实心球行进的高度y(m)与水平距离x(m)的函数表达式为y=-$\frac{1}{5}$x2+$\frac{7}{5}$x+$\frac{8}{5}$,则实心球落地时的水平距离是( )
| A. | 1m | B. | 8m | C. | 9m | D. | 10m |
3.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
则抛物线的对称轴是x=$\frac{1}{2}$.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
 如图所示,直线L1的解析式是y=2x-1,直线L2的解析式是y=x+1,则方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
如图所示,直线L1的解析式是y=2x-1,直线L2的解析式是y=x+1,则方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.