题目内容
20．
如图所示，直线L1的解析式是y=2x-1，直线L2的解析式是y=x+1，则方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$．
分析 二元一次方程组的解就是组成二元一次方程组的两个方程的公共解，即直线l1与l2的交点的坐标．
解答 解：根据题意知，
二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=1}\end{array}\right.$的解就是直线l1与l2的交点的坐标，
又∵交点坐标（2，3），
∴原方程组的解是：$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$．
故答案是：$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$
点评 本题考查了一次函数与二元一次方程组．二元一次方程组的解就是组成该方程组的两条直线的图象的交点．
练习册系列答案
相关题目
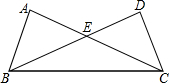如图，在Rt△ABC和Rt△BCD中，∠A=∠D=90°，AB=CD=4，BC=$4\sqrt{5}$，△BCE的面积=10．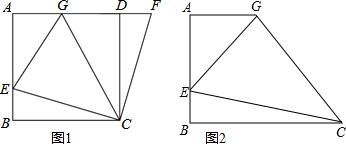
如图，一个正方形内两个相邻正方形的面积分别为4和2，它们都有两个顶点在大正方形的边上且组成的图形为轴对称图形，则图中阴影部分的面积为$\frac{3}{4}$+$\frac{9\sqrt{2}}{2}$．