题目内容
3．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
分析 首先找出纵坐标相等的两个点，可根据这两个点的横坐标判断出抛物线的对称轴．
解答 解：由抛物线过（0，6）、（1，6）两点知：
抛物线的对称轴为x=$\frac{0+1}{2}$=$\frac{1}{2}$．
故答案为：x=$\frac{1}{2}$．
点评 此题考查二次函数的性质，掌握二次函数的对称性，找出对称点是解决问题的关键．
练习册系列答案
华东师大版一课一练系列答案
相关题目
如图，已知∠AOB=60°，点P是OA边上，OP=8cm，点M、N在边OB上，PM=PN，若MN=2cm，则ON=5cm．
14．
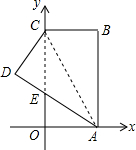如图，在平面直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC折叠，使点B落在D点的位置，且交y轴交于点E，则点D的坐标是（ ）
如图，在平面直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC折叠，使点B落在D点的位置，且交y轴交于点E，则点D的坐标是（ ）| A． | （-$\frac{3}{5}$，$\frac{8}{3}$） | B． | （-$\frac{3}{5}$，2） | C． | （-$\frac{4}{5}$，$\frac{14}{5}$） | D． | （-$\frac{4}{5}$，$\frac{12}{5}$） |
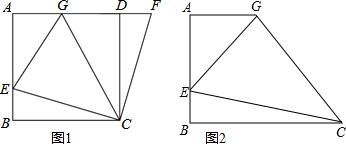
如图，一个正方形内两个相邻正方形的面积分别为4和2，它们都有两个顶点在大正方形的边上且组成的图形为轴对称图形，则图中阴影部分的面积为$\frac{3}{4}$+$\frac{9\sqrt{2}}{2}$．