题目内容
4.如果把两条邻边中较短边与较长边的比值为$\frac{\sqrt{5}-1}{2}$的矩形称作黄金矩形.现将长度为20cm的铁丝折成一个黄金矩形,这个黄金矩形较短的边长是15-5$\sqrt{5}$cm.分析 设这个黄金矩形较长的边长是xcm,根据长方形的周长公式列出算式求出x的值,再根据黄金分割的定义即可得出这个黄金矩形较短的边长.
解答 解:设这个黄金矩形较长的边长是xcm,根据题意得:
2(x+$\frac{\sqrt{5}-1}{2}$x)=20,
解得:x=5$\sqrt{5}$-5,
则这个黄金矩形较短的边长是$\frac{\sqrt{5}-1}{2}$×(5$\sqrt{5}$-5)=(15-5$\sqrt{5}$)cm.
故答案为:15-5$\sqrt{5}$.
点评 本题考查了黄金分割的定义:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值($\frac{\sqrt{5}-1}{2}$)叫做黄金比.同时考查了矩形的周长公式.

练习册系列答案
相关题目
14.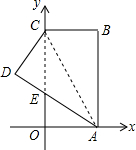 如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC折叠,使点B落在D点的位置,且交y轴交于点E,则点D的坐标是( )
如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC折叠,使点B落在D点的位置,且交y轴交于点E,则点D的坐标是( )
 如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC折叠,使点B落在D点的位置,且交y轴交于点E,则点D的坐标是( )
如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC折叠,使点B落在D点的位置,且交y轴交于点E,则点D的坐标是( )| A. | (-$\frac{3}{5}$,$\frac{8}{3}$) | B. | (-$\frac{3}{5}$,2) | C. | (-$\frac{4}{5}$,$\frac{14}{5}$) | D. | (-$\frac{4}{5}$,$\frac{12}{5}$) |
 如图,一个正方形内两个相邻正方形的面积分别为4和2,它们都有两个顶点在大正方形的边上且组成的图形为轴对称图形,则图中阴影部分的面积为$\frac{3}{4}$+$\frac{9\sqrt{2}}{2}$.
如图,一个正方形内两个相邻正方形的面积分别为4和2,它们都有两个顶点在大正方形的边上且组成的图形为轴对称图形,则图中阴影部分的面积为$\frac{3}{4}$+$\frac{9\sqrt{2}}{2}$.