题目内容
12.配方法解一元二次方程ax2+bx-c=0(a≠0,c>0)得到(x-c)2=4c2,从而解得方程一根为1,则a-3b=-3.分析 由(x-c)2=4c2可得x=-c或x=3c,根据方程一根为1且c>0得c=$\frac{1}{3}$,将其代入(x-c)2=4c2并整理可得x2-$\frac{2}{3}$x-$\frac{1}{3}$=0,从而得知a、b的值,即可得答案.
解答 解:由(x-c)2=4c2可得x-c=±2c,
∴x=c±2c,
即x=-c或x=3c,
∵方程一根为1,且c>0,
则3c=1,即c=$\frac{1}{3}$,
∴原方程为(x-$\frac{1}{3}$)2=$\frac{4}{9}$,
整理得:x2-$\frac{2}{3}$x-$\frac{1}{3}$=0,
∵c>0,
∴a=-1,b=$\frac{2}{3}$,
∴a-3b=-1-2=-3,
故答案为:-3.
点评 本题主要考查一元二次方程的解法和一元二次方程的解的定义,解题的关键是解方程并根据方程的解得定义得出c的值是关键.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
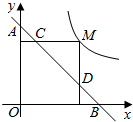 M为双曲线y=$\frac{\sqrt{3}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B.
M为双曲线y=$\frac{\sqrt{3}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B.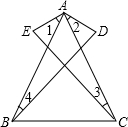 如图,∠3=∠4,AE=AD,∠1=∠2.求证:AC=AB.
如图,∠3=∠4,AE=AD,∠1=∠2.求证:AC=AB.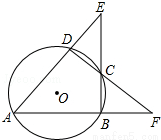 如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F. 实验与探究:三角点阵前n行的点数计算.
实验与探究:三角点阵前n行的点数计算.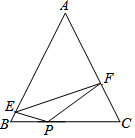 已知:如图,在△ABC中,AB=AC且tanA=$\frac{4}{3}$,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=2$\sqrt{13}$.
已知:如图,在△ABC中,AB=AC且tanA=$\frac{4}{3}$,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=2$\sqrt{13}$.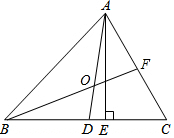 如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠ABC=45°,∠C=75°,求∠DAE,∠AOB的度数.
如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠ABC=45°,∠C=75°,求∠DAE,∠AOB的度数.
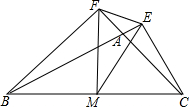 如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.
如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.