题目内容

17．a1、a2、a3、a5、a6是1、2、3、4、5、6的一个排列，若S=|a1-a2|+|a3-a4|+|a5-a6|，那么（　　）
A．S一定是一个奇数B．S一定是一个偶数
C．S可能是奇数也可能是偶数D．以上说法都不对

分析 由于a1、a2、a3、a5、a6是3奇3偶，则S=|a1-a2|+|a3-a4|+|a5-a6|可能是奇奇，奇偶，偶偶；奇偶，奇偶，奇偶；依此可得S=|a1-a2|+|a3-a4|+|a5-a6|的奇偶性．

解答 解：∵a1、a2、a3、a5、a6是1、2、3、4、5、6的一个排列，
∴S=|a1-a2|+|a3-a4|+|a5-a6||可能是奇奇，奇偶，偶偶；奇偶，奇偶，奇偶；
∴S一定是一个奇数．
故选：A．

点评 此题考查了绝对值，奇数和偶数的性质，关键是得到S=|a1-a2|+|a3-a4|+|a5-a6|可能是奇奇，奇偶，偶偶；奇偶，奇偶，奇偶2种情况．

练习册系列答案
相关题目
7．实验与探究：三角点阵前n行的点数计算．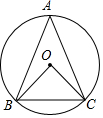
如图是一个三角点阵，从上向下数有无数多行，其中第一行有1个点，第二行有2个点…第n行有n个点…容易发现，10是三角点阵中前4行的点数的和，你能发现300是前多少行的点数的和吗？
如果要用试验的方法，由上而下地逐行的相加其点数，虽然你能发现1+2+3+4+…+23+24=300．得知300是前24行的点数的和，但是这样寻找答案需我们先探求三角点阵中前n行的点数的和与n的数量关系前n行的点数的和是1+2+3+…+（n-2）+（n-1）+n，可以发现．
2×[1+2+3+…+（n-2）+（n-1）+n]=[1+2+3+…+（n-2）+（n-1）+n]+[n+（n-1）+（n-2）+…3+2+1]
把两个中括号中的第一项相加，第二项相加…第n项相加，上式等号的后边变形为这n个小括号都等于n+1，整个式子等于n（n+1），于是得到1+2+3+…+（n-2）+（n-1）+n=n（n+1）这就是说，三角点阵中前n项的点数的和是 n（n+1）．
下列用一元二次方程解决上述问题
设三角点阵中前n行的点数的和为300，则有$\frac{1}{2}$n（n+1）=300整理这个方程，得：n2+n-600=0解方程得：n1=24，n2=-25，根据问题中未知数的意义确定n=24，即三角点阵中前24行的点数的和是300．请你根据上述材料回答下列问题：
（1）三角点阵中前n行的点数的和能是600吗？如果能，求出n；如果不能，试用一元二次方程说明道理．（2）如果把图中的三角点阵中各行的点数依次换成2、4、6、…、2n、…，你能探究出前n行的点数的和满足什么规律吗？这个三角点阵中前n行的点数的和能是600吗？如果能，求出n；如果不能，试用一元二次方程说明道理．
8．如图，在⊙O中，AB=AC，∠ABC=70°．∠BOC=80°．
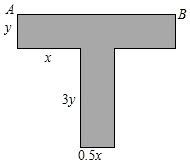5．某种T型零件尺寸如图所示（左右宽度相同），求：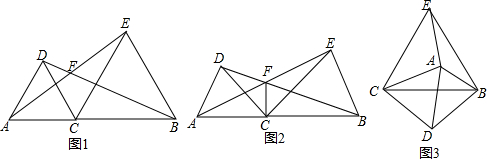
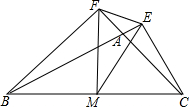（1）阴影部分的周长是多少？（用含x，y的代数式表示）
（2）阴影部分的面积是多少？（用含x，y的代数式表示）
（3）x=2，y=3.5时，计算阴影部分的面积．
12．已知点C为线段AB上一点，分别以AC、BC为边在线段AB同侧作△ACD和△BCE，且CA=CD，CB=CE，∠ACD=∠BCE，直线AE与BD交于点F．

（1）如图1，若∠ACD=60°，则∠AFD=60°；
（2）如图2，若∠ACD=α，连接CF，则∠AFC=90°-$\frac{1}{2}α$（用含α的式子表示）；
（3）将图1中的△ACD绕点C顺时针旋转如图3，连接AE、AB、BD，∠ABD=80°，求∠EAB的度数．
2．如图，在△ABC中，CE⊥BA的延长线于E，BF⊥CA的延长线于F，M为BC的中点，分别连接ME、MF、EF．
（1）若EF=3，BC=10，求△EFM的周长；
（2）若∠ABC=29°，∠ACB=46°，求∠EMF的度数．
9．平面上有四个点A、B、C、D，按照以下要求作图：
（1）连接AB并延长AB至E，使BE=AB；
（2）作射线CB；
（3）在直线BD上确定点G，使得AG+GC最短．
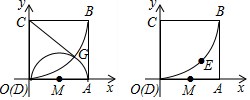6．如图，正方形ABCD的顶点A，C分别在x轴，y轴正半轴上，点B的坐标为（10，10），以点C为圆心，CB为半径画弧OB．
（1）以OA为直径的半圆M与弧OB交于点G，连接CG．
①判断CG与⊙M的位置关系，并证明你的结论；
②求G的坐标．
（2）设E（a，b）是$\widehat{OB}$上一动点，且a、b是方程x2-8x+k=0的两根，求k的值．
7．化简（3y-2x）3•（2x-3y）2n+1÷（3y-2x）2n+2（n为正整数）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网