题目内容
11.边长为8,一个内角为150°的菱形的面积为32.分析 作AM⊥BC于M,由菱形的性质得出AB=BC=2,AD∥BC,得出∠B=30°,由含30°角的直角三角形的性质求出AM=1,即可得出菱形的面积.
解答 解:如图所示: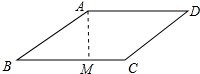
作AM⊥BC于M,则∠AMB=90°,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA=8,AD∥BC,
∴∠B+∠BAD=180°,
∴∠B=180°-150°=30°,
∴AM=$\frac{1}{2}$AB=4,
∴菱形ABCD的面积=BC•AM=8×4=32.
故答案为:32.
点评 本题考查了菱形的性质、含30°角的直角三角形的性质、菱形面积的计算;熟练掌握菱形的性质,由含30°角的直角三角形的性质求出菱形的高是解决问题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
20.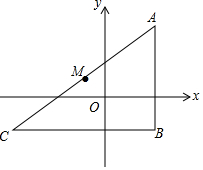 如图,在Rt△ABC中,∠B=90°,AB垂直于x轴,M为AC的中点,若点A的坐标为(3,4),点M的坐标为(-1,1),则点B的坐标为( )
如图,在Rt△ABC中,∠B=90°,AB垂直于x轴,M为AC的中点,若点A的坐标为(3,4),点M的坐标为(-1,1),则点B的坐标为( )
 如图,在Rt△ABC中,∠B=90°,AB垂直于x轴,M为AC的中点,若点A的坐标为(3,4),点M的坐标为(-1,1),则点B的坐标为( )
如图,在Rt△ABC中,∠B=90°,AB垂直于x轴,M为AC的中点,若点A的坐标为(3,4),点M的坐标为(-1,1),则点B的坐标为( )| A. | (3,-4) | B. | (3,-3) | C. | (3,-2) | D. | (3,-1) |

 如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.
如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF. 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论: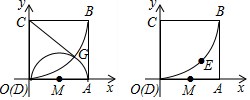 如图,正方形ABCD的顶点A,C分别在x轴,y轴正半轴上,点B的坐标为(10,10),以点C为圆心,CB为半径画弧OB.
如图,正方形ABCD的顶点A,C分别在x轴,y轴正半轴上,点B的坐标为(10,10),以点C为圆心,CB为半径画弧OB.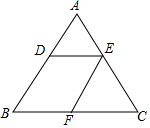 已知:如图,△ABC中,DE∥BC.
已知:如图,△ABC中,DE∥BC.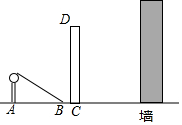 如图,小高同学在太阳光下的影子是线段AB.小高身高为1.6m,其影长是2m.
如图,小高同学在太阳光下的影子是线段AB.小高身高为1.6m,其影长是2m. 如图,直线y=x-$\sqrt{2}$与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,已知AO=AC.
如图,直线y=x-$\sqrt{2}$与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,已知AO=AC.