题目内容
10.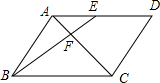 如图,点E是平行四边形ABCD的边AD上的中点,AC、BE相交于点F,则S△AEF:S△CBF=( )
如图,点E是平行四边形ABCD的边AD上的中点,AC、BE相交于点F,则S△AEF:S△CBF=( )| A. | 1:4 | B. | 1:2 | C. | 1:9 | D. | 4:1 |
分析 根据平行四边形的性质得到AD=BC,AD∥BC,由点E是AD的中点,得到AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,通过△AEF∽△BCF,根据相似三角形的性质得到$\frac{EF}{BF}=\frac{AE}{BC}$=$\frac{1}{2}$,于是得到结论.
解答 解:在?ABCD中,
∵AD=BC,AD∥BC,
∵点E是AD的中点,
∴AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∵AD∥BC,
∴△AFE∽△BCF,
∴$\frac{EF}{BF}=\frac{AE}{BC}$=$\frac{1}{2}$,
∴S△AFE:S△CFB=($\frac{EF}{BF}$)2=$\frac{1}{4}$,
故选A.
点评 此题考查了相似三角形的判定与性质以及平行四边形的性质.此题难度不大,注意掌握相似三角形面积的比等于相似比的平方定理的应用是解此题的关键.

练习册系列答案
相关题目
2.公园路中学组织了一次教师踢毽子比赛,甲、乙两教研组每队各10人的比赛成绩如表(10分制):
(1)甲队成绩的中位数是9.5分,乙队成绩的众数是10 分.
(2)计算乙队的平均成绩和方差.
(3)已知甲队的成绩的方差是1.4,则成绩较为整齐的是乙 队.
| 甲 | 7 | 9 | 8 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 7 | 8 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)计算乙队的平均成绩和方差.
(3)已知甲队的成绩的方差是1.4,则成绩较为整齐的是乙 队.
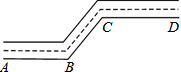 如图所示,一条街道的两个拐角∠ABC和∠BCD,若∠ABC=150°,当街道AB和CD平行时,∠BCD=150度,根据是两直线平行,内错角相等.
如图所示,一条街道的两个拐角∠ABC和∠BCD,若∠ABC=150°,当街道AB和CD平行时,∠BCD=150度,根据是两直线平行,内错角相等.