题目内容
 如图,在平面直角坐标系xOy中,K点坐标为(0,1),在抛物线y=x2-2x-3中,D是顶点,是否存在点L,使△AKL和△LCD面积相等?若有,求出点L坐标.
如图,在平面直角坐标系xOy中,K点坐标为(0,1),在抛物线y=x2-2x-3中,D是顶点,是否存在点L,使△AKL和△LCD面积相等?若有,求出点L坐标.考点:二次函数的性质
专题:计算题
分析:KA和DC的延长线相交于P,作PE⊥y轴于E,交抛物线于L和L′,作DH⊥y轴于H,先根据抛物线与x轴的交点问题确定A点坐标为(-1,0),易得△OKA为等腰直角三角形,则∠AKO=45°,利用配方得y=x2-2x-3=(x-1)2-4,得到D点坐标为(1,-4),则DH=1,CH=1,所以△CDH为等腰直角三角形,得到∠HCD=45°,根据对顶角相等得∠PCO=45°,于是可判断△PKC为等腰直角三角形,根据等腰直角三角形的性质得PE平分∠KPC,KE=CE,根据角平分线的性质得点L(或L′)到AK和CD的距离相等,所以△AKL和△LCD面积相等;然后确定直线PE为y=-1,再求直线y=-1与抛物线y=x2-2x-3的交点坐标即可.
解答:解:存在.
KA和DC的延长线相交于P,作PE⊥y轴于E,交抛物线于L和L′,作DH⊥y轴于H,如图,
把y=0代入y=x2-2x-3得x2-2x-3=0,解得x1=-1,x2=3,
∴A点坐标为(-1,0),
∵K(0,1),
∴△OKA为等腰直角三角形,
∴∠AKO=45°,
∵y=x2-2x-3=(x-1)2-4,
∴D点坐标为(1,-4),
而C(0,-3),
∴DH=1,CH=1,
∴△CDH为等腰直角三角形,
∴∠HCD=45°,
∴∠PCO=45°,
∴△PKC为等腰直角三角形,
∴PE平分∠KPC,KE=CE,
∴点L(或L′)到AK和CD的距离相等,
∵KC=4,
∴直线PE为y=-1,
把y=-1代入y=x2-2x-3得x2-2x-3=-1,解得x1=1-
,x2=1+
,
∴点L坐标为(1-
,-1)和(1+
,-1).
KA和DC的延长线相交于P,作PE⊥y轴于E,交抛物线于L和L′,作DH⊥y轴于H,如图,

把y=0代入y=x2-2x-3得x2-2x-3=0,解得x1=-1,x2=3,
∴A点坐标为(-1,0),
∵K(0,1),
∴△OKA为等腰直角三角形,
∴∠AKO=45°,
∵y=x2-2x-3=(x-1)2-4,
∴D点坐标为(1,-4),
而C(0,-3),
∴DH=1,CH=1,
∴△CDH为等腰直角三角形,
∴∠HCD=45°,
∴∠PCO=45°,
∴△PKC为等腰直角三角形,
∴PE平分∠KPC,KE=CE,
∴点L(或L′)到AK和CD的距离相等,
∵KC=4,
∴直线PE为y=-1,
把y=-1代入y=x2-2x-3得x2-2x-3=-1,解得x1=1-
| 3 |
| 3 |
∴点L坐标为(1-
| 3 |
| 3 |
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,对称即顶点是抛物线的最低点;当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.也考查了等腰直角三角形的判定与性质.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
下列各式的计算中不正确的个数是( )
(1)100÷10-1=10;
(2)10-4•(2×7)0=1000;
(3)(0.1)0÷(-
)-3=8;
(4)(-10)-4÷(-
)-4=-1.
(1)100÷10-1=10;
(2)10-4•(2×7)0=1000;
(3)(0.1)0÷(-
| 1 |
| 2 |
(4)(-10)-4÷(-
| 1 |
| 10 |
| A、4个 | B、3个 | C、2个 | D、1个 |
已知9x2+kxy+4y2是一个完全平方展开式,那么k的值是( )
| A、12 | B、24 |
| C、±12 | D、±24 |
 如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2cm/s的速度移动,点Q沿DA边从D开始向A以1cm/s的速度移动,如果P、Q同时出发,用t表示时间(0≤t≤6)则:
如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2cm/s的速度移动,点Q沿DA边从D开始向A以1cm/s的速度移动,如果P、Q同时出发,用t表示时间(0≤t≤6)则: 设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.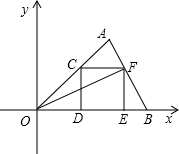 如图,在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
如图,在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t. 如图所示,在⊙O中,PA切⊙O于A,AD平分∠BAC,PE平分∠APB,AD=4cm,PA=6cm.求EP的长.
如图所示,在⊙O中,PA切⊙O于A,AD平分∠BAC,PE平分∠APB,AD=4cm,PA=6cm.求EP的长.