题目内容
14.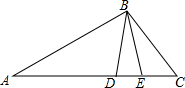 如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE.
如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE.
分析 利用比例性质由AB2=AD•AC得出$\frac{AB}{AC}$=$\frac{AD}{AB}$,然后加上公共角,证明△ADB∽△ABC,得出∠ABD=∠C,再由角平分线的定义和三角形的外角性质证出∠ABE=∠AEB,得出AB=AE即可.
解答 证明:∵AB2=AD•AC,
∴$\frac{AB}{AC}$=$\frac{AD}{AB}$,
又∵∠A=∠A,
∴△ADB∽△ABC,
∴∠ABD=∠C,
∵AC平分∠CBD,
∴∠DBE=∠CBE,
∵∠ABE=∠ABD+∠DBE,∠AEB=∠CBE+∠C,
∴∠ABE=∠AEB,
∴AB=AE.
点评 本题考查了相似三角形的判定与性质、三角形的外角性质、等腰三角形的判定;证明三角形相似是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC的长为3.
如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC的长为3. 已知,如图,AB∥CD,∠ABE=80°,EF平分∠BEC,EF⊥EG,求∠DEG的度数.
已知,如图,AB∥CD,∠ABE=80°,EF平分∠BEC,EF⊥EG,求∠DEG的度数. 如图,△ABC≌△DEF,点A、B、C对应点为D、E、F,若BE=3,AE=1,则DE=4.
如图,△ABC≌△DEF,点A、B、C对应点为D、E、F,若BE=3,AE=1,则DE=4.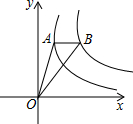 如图,点A是反比例函数y1=$\frac{1}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{k}{x}$(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为5.
如图,点A是反比例函数y1=$\frac{1}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{k}{x}$(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为5.