题目内容
9. 已知,如图,AB∥CD,∠ABE=80°,EF平分∠BEC,EF⊥EG,求∠DEG的度数.
已知,如图,AB∥CD,∠ABE=80°,EF平分∠BEC,EF⊥EG,求∠DEG的度数.
分析 首先由AB∥CD,∠ABE=80°,根据两直线平行,同旁内角互补,可求得∠BEC的度数,然后由EF平分∠BEC,求得∠CEF的度数,继而求得答案.
解答 解:∵AB∥CD,∠ABE=80°,
∴∠BEC=180°-∠ABE=100°,
∵EF平分∠BEC,
∴∠CEF=$\frac{1}{2}$∠BEC=50°,
∵EF⊥EG,
∴∠FEG=90°,
∴∠DEG=180°-∠CEF-∠FEG=40°.
点评 此题考查了平行线的性质以及角平分线的定义.注意掌握两直线平行,同旁内角互补定理的应用是解此题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
18.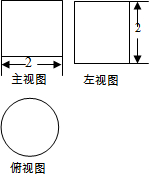 如图是某几何体的三视图,下列判断正确的是( )
如图是某几何体的三视图,下列判断正确的是( )
 如图是某几何体的三视图,下列判断正确的是( )
如图是某几何体的三视图,下列判断正确的是( )| A. | 几何体是圆柱体,高为2 | B. | 几何体是圆锥体,高为2 | ||
| C. | 几何体是圆柱体,半径为2 | D. | 几何体是圆锥体,直径为2 |
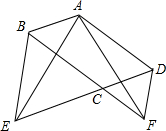 如图,在平行四边形ABCD中,∠BCD=120°,分别延长DC、BC到点E、F,使得△BCE和△CDF都是正三角形.求证:AE=AF.
如图,在平行四边形ABCD中,∠BCD=120°,分别延长DC、BC到点E、F,使得△BCE和△CDF都是正三角形.求证:AE=AF. 如图,已知AD∥BC,∠C=38°,∠ADB:∠BDC=1:3,则∠ADB=35.5°.
如图,已知AD∥BC,∠C=38°,∠ADB:∠BDC=1:3,则∠ADB=35.5°. 如图,图中所有的四边形都是正方形,所有的三角形都是直角三角形,已知正方形A、B、C、D的边长分别是12,16,9,12,则最大正方形E的面积是625.
如图,图中所有的四边形都是正方形,所有的三角形都是直角三角形,已知正方形A、B、C、D的边长分别是12,16,9,12,则最大正方形E的面积是625.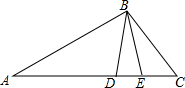 如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE.
如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE.