题目内容
3.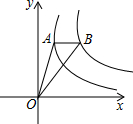 如图,点A是反比例函数y1=$\frac{1}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{k}{x}$(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为5.
如图,点A是反比例函数y1=$\frac{1}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{k}{x}$(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为5.
分析 延长BA,与y轴交于点C,由AB与x轴平行,得到BC垂直于y轴,利用反比例函数k的几何意义表示出三角形AOC与三角形BOC面积,由三角形BOC面积减去三角形AOC面积表示出三角形AOB面积,将已知三角形AOB面积代入求出k的值即可.
解答  解:延长BA,与y轴交于点C,
解:延长BA,与y轴交于点C,
∵AB∥x轴,
∴BC⊥y轴,
∵A是反比例函数y1=$\frac{1}{x}$(x>0)图象上一点,B为反比例函数y2=$\frac{k}{x}$(x>0)的图象上的点,
∴S△AOC=$\frac{1}{2}$,S△BOC=$\frac{k}{2}$,
∵S△AOB=2,即$\frac{k}{2}$-$\frac{1}{2}$=2,
解得:k=5,
故答案为:5
点评 此题考查了反比例函数k的几何意义,熟练掌握反比例函数k的几何意义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.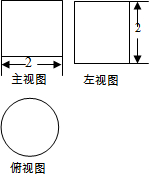 如图是某几何体的三视图,下列判断正确的是( )
如图是某几何体的三视图,下列判断正确的是( )
 如图是某几何体的三视图,下列判断正确的是( )
如图是某几何体的三视图,下列判断正确的是( )| A. | 几何体是圆柱体,高为2 | B. | 几何体是圆锥体,高为2 | ||
| C. | 几何体是圆柱体,半径为2 | D. | 几何体是圆锥体,直径为2 |
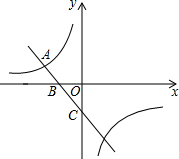 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a).
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a).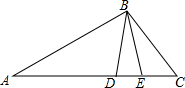 如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE.
如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE.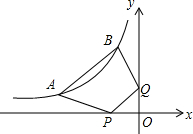 如图,点A(a,1)、B(-1,b)都在函数$y=-\frac{3}{x}$(x<0)的图象上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是y=x+2.
如图,点A(a,1)、B(-1,b)都在函数$y=-\frac{3}{x}$(x<0)的图象上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是y=x+2. 反比例函数y=$\frac{k}{x}$在第一象限的图象如图,请写出一个满足条件的k值,k=3.
反比例函数y=$\frac{k}{x}$在第一象限的图象如图,请写出一个满足条件的k值,k=3.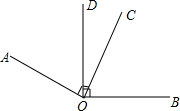 如图,若AO⊥OC,BO⊥DO,
如图,若AO⊥OC,BO⊥DO, 如图,AB与CD相交于点O,∠AOD+∠BOC=280°,则∠AOC=40°.
如图,AB与CD相交于点O,∠AOD+∠BOC=280°,则∠AOC=40°.