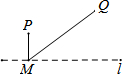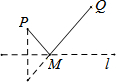题目内容
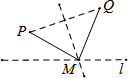
3.(1)将两块等腰直角三角板AOB和COD按如图①放置,其中∠AOB=∠COD=90°,求证:AC=BD.(2)将两块含30°的直角三角板AOB和COD按如图②放置,其中∠AOB=∠COD=90°,∠OAB=∠OCD=30°,求证:BD⊥AC.
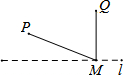
(3)将图②的三角板OCD绕点O旋转到点C,D,B三点一线时如图③所示,若AB=14,CD=10,求sin∠AOC的值.
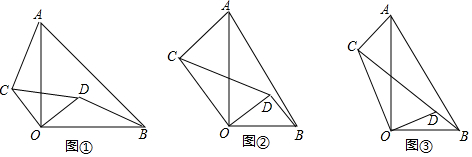
分析 (1)由等腰直角三角形的性质得出OC=OD,OA=OB,再判断出∠AOC=∠BOD,即可得出△AOC≌△BOD即可;
(2)根据含30°的直角三角形的性质判断出$\frac{OC}{OA}=\frac{OD}{OB}$,再判断出∠AOC=∠BOD,即可得出△AOC∽△BOD,即可得出∠CAO=∠DBO,最后用等量代换求出∠CAB+ABE=90°,即可;
(3)先利用(2)的结论求出BD=3,再利用含30°的直角三角形的性质得出OB=7,OD=5,最后用勾股定理求出DF即可得出结论.
解答 解:(1)∵两块等腰直角三角板AOB和COD,
∴OA=OB,OC=OD,
∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
在△AOC和△BOD中,$\left\{\begin{array}{l}{OA=OB}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$,
∴△AOC≌△BOD,
∴AC=BD;
(2)如图②,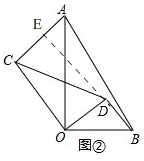 延长BD交AC于E,
延长BD交AC于E,
在Rt△AOB中,∠OAB=30°,
∴AB=2OB,OA=$\sqrt{3}$OB,
同理:OC=$\sqrt{3}$OD,
∴$\frac{OC}{OA}=\frac{\sqrt{3}OD}{\sqrt{3}OB}$=$\frac{OD}{OB}$,
∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
∴△AOC∽△BOD,
∴∠CAO=∠DBO,
∴∠CAB+∠ABE=∠CAO+∠OAB+∠ABE=∠DBO+∠ABE+∠OAB=ABO+∠OAB=90°,
∴∠AEB=90°,
∴BD⊥AC;
(3)如图③,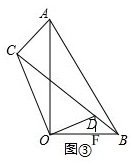 过点D作DF⊥OB于F,
过点D作DF⊥OB于F,
由(2)知,BC⊥AC,△AOC∽△BOD,
∴$\frac{AC}{BD}=\frac{OA}{OB}=\frac{\sqrt{3}}{1}$,
∴AC=$\sqrt{3}$BD,
在Rt△ABC中,AB=14,BC=CD+BD=10+BD,
根据勾股定理得,BC2+AC2=AB2,
∴(10+BD)2+($\sqrt{3}$BD)2=142,
∴BD=-8(舍)或BD=3,
在Rt△AOB中,AB=14,∠OAB=30°,∴OB=7,
在Rt△COD中,CD=10,∠OCD=30°,∴OD=5,
在Rt△ACF中,DF2=BD2-BF2=BD2-(OB-OF)2=9-(7-OF)2,
在Rt△OCF中,DF2=OD2-OF2=25-OF2,
∴9-(7-OF)2=25-OF2,
∴OF=$\frac{65}{14}$,
∴DF=$\frac{15\sqrt{3}}{14}$,
∴在Rt△ODF中,sin∠AOC=sin∠DOF=$\frac{DF}{OD}=\frac{\frac{15\sqrt{3}}{14}}{5}$=$\frac{3\sqrt{3}}{14}$.
点评 此题是三角形综合题,主要考查了等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,含30°角的直角三角形的性质,勾股定理;解(1)的关键是判断出∠AOC=∠BOD,解(2)的关键是判断出$\frac{OC}{OA}=\frac{OD}{OB}$,解(3)的关键是利用勾股定理求出线段的长.

 金状元绩优好卷系列答案
金状元绩优好卷系列答案| A. | 6.75×103吨 | B. | 6.75×10-4吨 | C. | 6.75×105吨 | D. | 6.75×104吨 |
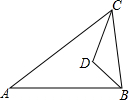 如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D:∠A=7:2,则∠A的度数是( )
如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D:∠A=7:2,则∠A的度数是( )| A. | 30° | B. | 32° | C. | 36° | D. | 40° |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
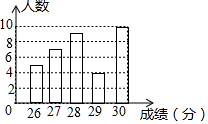 如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )
如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )| A. | 28分,30分 | B. | 28.5分,30分 | C. | 27.5分,28分 | D. | 28.2分,30分 |
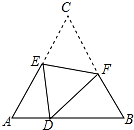 如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )
如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )| A. | $\frac{5}{3}$ | B. | $\frac{7}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{3}{5}$ |
| A. | a4•a=a4 | B. | a6-a3=a3 | C. | (ab2)3=a3•b5 | D. | (a3)2=a6 |