题目内容
11.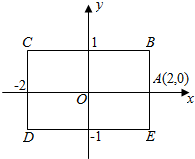 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是( )| A. | (2,0) | B. | (-1,1) | C. | (-2,1) | D. | (-1,-1) |
分析 利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每一次相遇的地点,找出规律即可解答.
解答 解:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×$\frac{1}{3}$=4,物体乙行的路程为12×$\frac{2}{3}$=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×$\frac{1}{3}$=8,物体乙行的路程为12×2×$\frac{2}{3}$=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×$\frac{1}{3}$=12,物体乙行的路程为12×3×$\frac{2}{3}$=24,在A点相遇;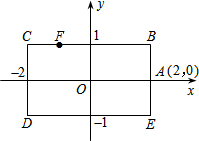
此时甲乙回到原出发点,
则每相遇三次,甲乙两物体回到出发点,
∵2017÷3=672…1,
故两个物体运动后的第2014次相遇地点的是:第一次相遇地点,
即物体甲行的路程为12×1×$\frac{1}{3}$=4,物体乙行的路程为12×1×$\frac{2}{3}$=8;
此时相遇点F的坐标为:(-1,1),
故选:B.
点评 此题主要考查了点的变化规律以及行程问题中的相遇问题及按比例分配的运用,通过计算发现规律就可以解决问题.解本题的关键是找出规律每相遇三次,甲乙两物体回到出发点.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
1.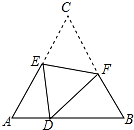 如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )
如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )
 如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )
如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )| A. | $\frac{5}{3}$ | B. | $\frac{7}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{3}{5}$ |
19. 如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
 如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )| A. | ∠A=∠D | B. | ∠ACB=∠DFE | C. | AC=DF | D. | BE=CF |
6.下列等式中成立的是( )
| A. | a4•a=a4 | B. | a6-a3=a3 | C. | (ab2)3=a3•b5 | D. | (a3)2=a6 |
16. 如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )
如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )
 如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )
如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )| A. | 6 cm2 | B. | 8 cm2 | C. | 10 cm2 | D. | 12 cm2 |
20.下列调查的样本选取方式,最具有代表性的是( )
| A. | 在青少年中调查年度最受欢迎的男歌手 | |
| B. | 了解班上学生的睡眠时间.调查班上学号为双号的学生的睡眠时间 | |
| C. | 为了了解你所在学校的学生每天的上网时间,向八年级的同学进行调查 | |
| D. | 对某市的出租司机进行体检,以此反映该市市民的健康状况 |
1.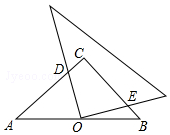 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )
 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{6}$ |