题目内容
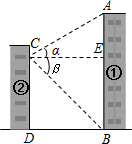 某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.在活动中,某小组为了测量校园内①号楼AB的高度(如图),站在②号楼的C处,测得①号楼顶部A处的仰角α=30°,底部B处的俯角β=45°,已知两幢楼的水平距离BD为18米,求①号楼AB的高度.(结果保留根号)
某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.在活动中,某小组为了测量校园内①号楼AB的高度(如图),站在②号楼的C处,测得①号楼顶部A处的仰角α=30°,底部B处的俯角β=45°,已知两幢楼的水平距离BD为18米,求①号楼AB的高度.(结果保留根号)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:根据在Rt△BCE中,tan∠BCE=
,求出BE的值,再根据在Rt△ACE中,tan∠ACE=
,求出AE的值,最后根据AB=AE+BE,即可求出答案.
| BE |
| CE |
| AE |
| CE |
解答:解:∵AB⊥BD,CD⊥BD,CE⊥AB,
∴四边形CDBE是矩形,
∴CE=BD=18.
在Rt△BEC中,∵∠ECB=45°,
∴EB=CE=18.
在Rt△AEC中,∵tan∠ACE=
,
∴AE=CE•tan∠ACE=18×tan 30°=6
,
∴AB=AE+EB=18+6
.
答:①号楼AB的高为(18+6
)米.
∴四边形CDBE是矩形,
∴CE=BD=18.
在Rt△BEC中,∵∠ECB=45°,
∴EB=CE=18.
在Rt△AEC中,∵tan∠ACE=
| AE |
| CE |
∴AE=CE•tan∠ACE=18×tan 30°=6
| 3 |
∴AB=AE+EB=18+6
| 3 |
答:①号楼AB的高为(18+6
| 3 |
点评:此题考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
将点A(3,2)向左平移4个单位长度得到点B,则点B所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
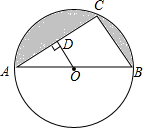 如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5.
如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5. 如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒). 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=80cm,则截面圆的半径为
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=80cm,则截面圆的半径为