题目内容
定义:点P为△ABC内部或边上的点,若满足△PAB,△PBC,△PAC至少有一个三角形与△ABC相似(点P不与△ABC顶点重合),则称点P为△ABC的自相似点.
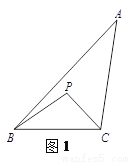
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
在平面直角坐标系xOy中,
(1)点A坐标为(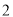 ,
, 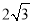 ), AB⊥x轴于B点,在E(2,1),F (
), AB⊥x轴于B点,在E(2,1),F (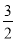 ,
, 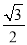 ),G (
),G (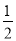 ,
, 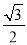 ),这三个点中,其中是△AOB的自相似点的是 (填字母);
),这三个点中,其中是△AOB的自相似点的是 (填字母);
(2)若点M是曲线C: 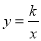 (
(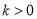 ,
, 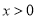 )上的一个动点,N为x轴正半轴上一个动点;
)上的一个动点,N为x轴正半轴上一个动点;
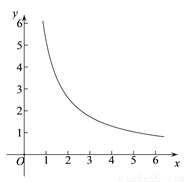 图2
图2
① 如图2, 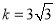 ,M点横坐标为3,且NM = NO,若点P是△MON的自相似点,求点P的坐标;
,M点横坐标为3,且NM = NO,若点P是△MON的自相似点,求点P的坐标;
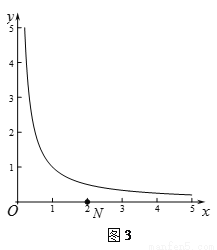
②若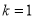 ,点N为(2,0),且△MON的自相似点有2个,则曲线C上满足这样条件的点M共有 个,请在图3中画出这些点(保留必要的画图痕迹).
,点N为(2,0),且△MON的自相似点有2个,则曲线C上满足这样条件的点M共有 个,请在图3中画出这些点(保留必要的画图痕迹).
练习册系列答案
相关题目

 .
. 中,直径
中,直径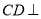 弦
弦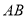 ,则下列结论中正确的是( )
,则下列结论中正确的是( )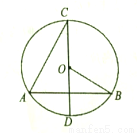
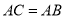 B.
B. 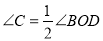 C.
C.  D.
D. 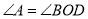
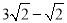 的值是( )
的值是( )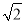 D. 2
D. 2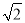
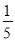 ,
, 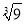 ,
, 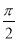 ,3.14,-
,3.14,- 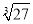 ,0,-5.123 45…,
,0,-5.123 45…,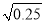 ,-
,- 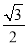 .
.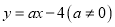 与双曲线
与双曲线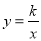 只有一个公共点A(1,
只有一个公共点A(1, 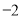 ).
).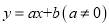 与双曲线
与双曲线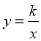 有两个公共点,请直接写出b的取值范围.
有两个公共点,请直接写出b的取值范围. 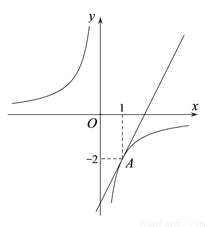
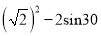 °
°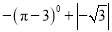 .
.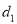 ,到y轴的距离为
,到y轴的距离为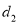 ,若
,若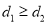 ,则称
,则称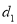 为点P的最大距离;若
为点P的最大距离;若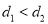 ,则称
,则称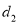 为点P的最大距离.
为点P的最大距离.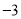 ,
, 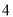 )到到x轴的距离为4,到y轴的距离为3,因为3<4,所以点P的最大距离为
)到到x轴的距离为4,到y轴的距离为3,因为3<4,所以点P的最大距离为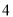 .
.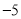 )的最大距离为________;
)的最大距离为________;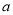 ,
, 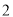 )的最大距离为
)的最大距离为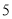 ,则
,则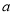 的值为________;
的值为________;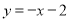 上,且点C的最大距离为
上,且点C的最大距离为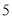 ,求点C的坐标;
,求点C的坐标;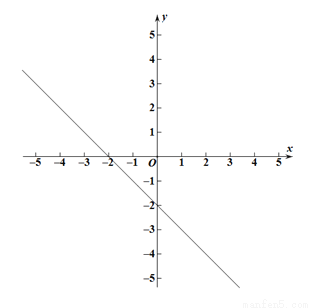
 ,直接写出⊙O的半径r的取值范围.
,直接写出⊙O的半径r的取值范围.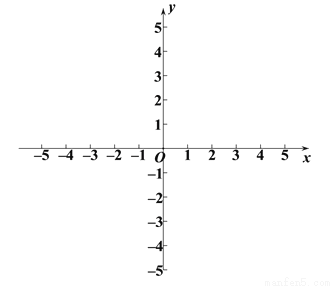
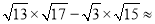 ________(计算结果保留两位小数).
________(计算结果保留两位小数).