题目内容
7．下列各式中计算正确的是（ ）| A． | （x+y）2=x2+y2 | B． | 3x2=6x2 | C． | a2+a2=a4 | D． | （x2）3=x6 |
分析 根据完全平方公式、同底数幂的乘法，合并同类项法则，幂的乘方分别求出每个式子的值，再判断即可．
解答 解：A、结果是x2+2xy+y2，故本选项不符合题意；
B、3x2和6x2不一定相等，故本选项不符合题意；
C、结果是2a2，故本选项不符合题意；
D、结果是x6，故本选项符合题意；
故选D．
点评 本题考查了完全平方公式，同底数幂的乘法，合并同类项法则，幂的乘方等知识点，能灵活运用法则进行计算是解此题的关键．
练习册系列答案
相关题目
如图，AB∥CD，AF∥ED，判断∠A与∠D是否相等，并说明理由．
2．已知m，n是方程x2-2x-1=0的两实数根，则$\frac{1}{m}$+$\frac{1}{n}$的值为（ ）
| A． | -2 | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | 2 |
12．
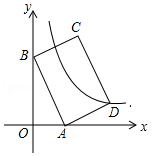如图，平面直角坐标系中，矩形ABCD的边AB：BC=3：2，点A（3，0），B（0，6）分别在x轴，y轴上，反比例函数y=$\frac{k}{x}$的图象经过点D，则k值为（ ）
如图，平面直角坐标系中，矩形ABCD的边AB：BC=3：2，点A（3，0），B（0，6）分别在x轴，y轴上，反比例函数y=$\frac{k}{x}$的图象经过点D，则k值为（ ）| A． | -14 | B． | 14 | C． | 7 | D． | -7 |
19．
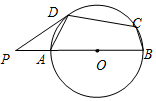如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=115°，过D点的切线PD与射线BA交于点P，则∠ADP的度数为（ ）
如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=115°，过D点的切线PD与射线BA交于点P，则∠ADP的度数为（ ）| A． | 25° | B． | 30° | C． | 35° | D． | 40° |
16．一元二次方程x2+x+0.25=0的根的情况是（ ）
| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 无实数根 | D． | 无法确定根的情况 |