题目内容
8.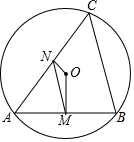 如图,△ABC内接于⊙O,OM⊥AB,ON⊥AC,垂足分别为M,N,连接MN,若AB=4,AC=6,∠A=60°.设MN=m,则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是( )
如图,△ABC内接于⊙O,OM⊥AB,ON⊥AC,垂足分别为M,N,连接MN,若AB=4,AC=6,∠A=60°.设MN=m,则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | $\frac{1}{2}$$\sqrt{3}$ | D. | $\frac{1}{2}\sqrt{2}$ |
分析 过C作CD⊥AB于D,解直角三角形得到CD=ACsin∠A=6sin60=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,AD=ACcos60°=6×$\frac{1}{2}$=3根据勾股定理得到BC=$\sqrt{C{D}^{2}+B{D}^{2}}$=$\sqrt{(3\sqrt{3})^{2}+{1}^{2}}$=2$\sqrt{7}$,
根据三角形的中位线的性质得到m=$\frac{1}{2}$BC=$\frac{1}{2}$×2$\sqrt{7}$=$\sqrt{7}$,于是得到结论.
解答 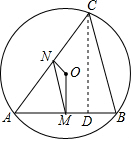 解:过C作CD⊥AB于D,
解:过C作CD⊥AB于D,
∵AC=6,∠A=60°,
∴CD=ACsin∠A=6sin60=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,AD=ACcos60°=6×$\frac{1}{2}$=3,
∴DB=AB-AD=1,
∴BC=$\sqrt{C{D}^{2}+B{D}^{2}}$=$\sqrt{(3\sqrt{3})^{2}+{1}^{2}}$=2$\sqrt{7}$,
∵OM⊥AB,ON⊥AC,
∴AM=MB,AN=NC,
∴MN=m=$\frac{1}{2}$BC=$\frac{1}{2}$×2$\sqrt{7}$=$\sqrt{7}$,
∴$\sqrt{{m}^{2}+1}$=$\sqrt{(\sqrt{7})^{2}+1}$=$\sqrt{8}$=2$\sqrt{2}$,
故选B.
点评 本题考查了垂径定理,三角形的中位线的性质,二次根式的化简,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
19.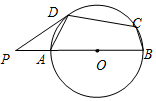 如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )
 如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
16.一元二次方程x2+x+0.25=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定根的情况 |