题目内容
已知△ABC中，BC=41，AC=40，AB=9，则此三角形为 三角形．
考点：勾股定理的逆定理
专题：
分析：由勾股定理的逆定理，可得此三角形是直角三角形．
解答：解：∵BC=41，AC=40，AB=9，
且92+402=412，
即：AB2+AC2=BC2
∴此三角形是直角三角形．
故答案为：直角．
且92+402=412，
即：AB2+AC2=BC2
∴此三角形是直角三角形．
故答案为：直角．
点评：本题考查勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．
练习册系列答案
相关题目
△ABC在直角坐标系中的位置如图所示，∠C=90°，点C的坐标为（| 3 |
| 2 |
| ||
| 2 |
A、（
| ||||
B、（
| ||||
C、（
| ||||
| D、（2，0） |
在Rt△ACB中，∠C=90°，sinB=
，则tanA=（ ）
| 1 |
| 5 |
A、
| ||||
B、
| ||||
C、2
| ||||
| D、24 |
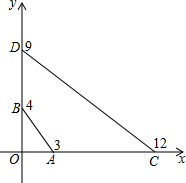已知如图，A，B，C，D四点的坐标分别是（3，0），（0，4），（12，0），（0，9），探索∠OBA和∠OCD的大小关系，并说明理由．
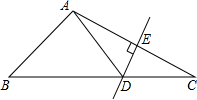如图，在△ABC中，DE是AC的垂直平分线，AE=4cm，△ABD的周长为12cm，求△ABC的周长．
如图是由五个大小相同的正方体搭成的几何体，从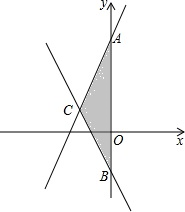
如图，已知直线y=2x+5和y=-x-1相交于点C，且两直线与y轴的交点分别是A，B．
已知：如图，在?ABCD中，从顶点D向AB作垂线，垂足为E，且E是AB的中点，已知?ABCD的周长为8.6cm，△ABD的周长为6cm．求AB、BC的长．