题目内容
 △ABC在直角坐标系中的位置如图所示,∠C=90°,点C的坐标为(
△ABC在直角坐标系中的位置如图所示,∠C=90°,点C的坐标为(| 3 |
| 2 |
| ||
| 2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,0) |
考点:解直角三角形,坐标与图形性质
专题:
分析:作CD⊥AB于D.由点C的坐标为(
,-
),得出AD=
,CD=
.解Rt△ACD,由tan∠CAD=
=
,得到∠CAD=30°,根据直角三角形两锐角互余求出∠CBD=90°-30°=60°.再解Rt△BCD,得出DB=
=
,那么AB=AD+DB=2,于是点B的坐标是(2,0).
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| CD |
| AD |
| ||
| 3 |
| CD |
| tan∠CBD |
| 1 |
| 2 |
解答: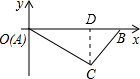 解:如图,作CD⊥AB于D.
解:如图,作CD⊥AB于D.
∵点C的坐标为(
,-
),
∴AD=
,CD=
.
在Rt△ACD中,∵∠ADC=90°,
∴tan∠CAD=
=
=
,
∴∠CAD=30°,
∵∠ACB=90°,
∴∠CBD=90°-30°=60°.
在Rt△BCD中,∵∠BDC=90°,
∴DB=
=
=
,
∴AB=AD+DB=
+
=2,
∴点B的坐标是(2,0).
故选D.
 解:如图,作CD⊥AB于D.
解:如图,作CD⊥AB于D.∵点C的坐标为(
| 3 |
| 2 |
| ||
| 2 |
∴AD=
| 3 |
| 2 |
| ||
| 2 |
在Rt△ACD中,∵∠ADC=90°,
∴tan∠CAD=
| CD |
| AD |
| ||||
|
| ||
| 3 |
∴∠CAD=30°,
∵∠ACB=90°,
∴∠CBD=90°-30°=60°.
在Rt△BCD中,∵∠BDC=90°,
∴DB=
| CD |
| tan∠CBD |
| ||||
|
| 1 |
| 2 |
∴AB=AD+DB=
| 3 |
| 2 |
| 1 |
| 2 |
∴点B的坐标是(2,0).
故选D.
点评:本题考查了解直角三角形,坐标与图形性质,锐角三角函数的定义,特殊角的三角函数值等知识,求出∠CAD=30°是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
三棱柱共有( )
| A、3条棱 | B、6条棱 |
| C、9条棱 | D、12条棱 |
 已知:如图,△ABC中,AB=AC,P是BC延长线上一点,PE⊥AB,PF⊥AC,CD⊥AB.求证:PE=CD+PF.
已知:如图,△ABC中,AB=AC,P是BC延长线上一点,PE⊥AB,PF⊥AC,CD⊥AB.求证:PE=CD+PF.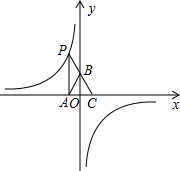 如图,点P是反比例函数y=
如图,点P是反比例函数y= 如图,OA=OC,请你添加一个条件:
如图,OA=OC,请你添加一个条件: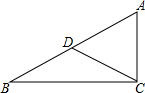 如图,∠ACB=90°,∠ADC=2∠B,AC=4,CD=3,求tan∠B.
如图,∠ACB=90°,∠ADC=2∠B,AC=4,CD=3,求tan∠B.