题目内容
8.计算:(1)$\frac{4x}{3y}$•$\frac{y}{2{x}^{3}}$
(2)$(\frac{y}{6{x}^{2}})^{2}$÷$(\frac{{y}^{2}}{4x})^{2}$
(3)化简:$\frac{(a-b)^{2}}{ab}$-$\frac{{a}^{2}-{b}^{2}}{ab}$
(4)化简:($\frac{1}{x-3}$-$\frac{x+1}{{x}^{2}-1}$)•(x-3)
分析 (1)原式约分即可得到结果;
(2)原式先计算乘方运算,再计算除法运算即可得到结果;
(3)原式利用同分母分式的减法法则计算,即可得到结果;
(4)原式利用乘法分配律计算即可得到结果.
解答 解:(1)原式=$\frac{2}{3{x}^{2}}$;
(2)原式=$\frac{{y}^{2}}{36{x}^{4}}$•$\frac{16{x}^{2}}{{y}^{4}}$=$\frac{4}{9{x}^{2}{y}^{2}}$;
(3)原式=$\frac{{a}^{2}-2ab+{b}^{2}-{a}^{2}+{b}^{2}}{ab}$=$\frac{2b(b-a)}{ab}$;
(4)原式=1-$\frac{(x+1)(x-3)}{(x+1)(x-1)}$=1-$\frac{x-3}{x-1}$=$\frac{x-1-x+3}{x-1}$=$\frac{2}{x-1}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.有六根细木条,它们的长度分别为3、8、12、15、17、18(单位:cm),从中取出三根首尾顺次连结搭成一个直角三角形,则这三根细木条的长度分别为( )
| A. | 3,8,12 | B. | 8,15,17 | C. | 12,15,18 | D. | 3,17,18 |
20.为了了解某市七年级学生的体重情况,相关人员抽查了该市1000名七年级学生,则下列说法中错误的是( )
| A. | 该市七年级学生的全体是总体 | |
| B. | 每个七年级学生的体重是个体 | |
| C. | 抽查的1000名学生的体重是总体的一个样本 | |
| D. | 这次调查样本的容量是1000 |
 如图,菱形OABC的顶点O在坐标原点,顶点B在x轴的正半轴上,OA边所在直线为y=$\frac{\sqrt{3}}{3}$x,AB边所在直线为y=-$\frac{\sqrt{3}}{3}$x+2.
如图,菱形OABC的顶点O在坐标原点,顶点B在x轴的正半轴上,OA边所在直线为y=$\frac{\sqrt{3}}{3}$x,AB边所在直线为y=-$\frac{\sqrt{3}}{3}$x+2.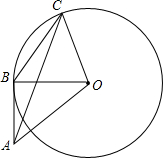 如图,AB是⊙O的切线,BC是⊙O的弦,且AB=BC=OB,求∠BAC的度数.
如图,AB是⊙O的切线,BC是⊙O的弦,且AB=BC=OB,求∠BAC的度数. 以点A为圆心的圆可表示为⊙A.如图所示,⊙A是由⊙B怎样平移得到的?对应圆心A、B的坐标有何变化?
以点A为圆心的圆可表示为⊙A.如图所示,⊙A是由⊙B怎样平移得到的?对应圆心A、B的坐标有何变化?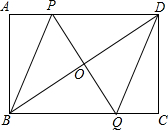 如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.