题目内容
18.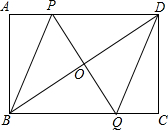 如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,点P从点A出发,以1cm/s的速度向点D运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;
(3)当t为何值时,四边形PBQD是菱形?
分析 (1)由矩形ABCD中,O为BD的中点,易证得△PDO≌△QBO(ASA),继而证得OP=OQ;
(2)AD=8cm,AP=tcm,即可用t表示PD的长;
(3)由四边形PBQD是菱形,可得PB=PD,即可得AB2+AP2=PD2,继而可得方程62+t2=(8-t)2,解此方程即可求得答案.
解答 解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
∵O为BD的中点,
∴DO=BO,
在△PDO和△QBO中,
$\left\{\begin{array}{l}{∠PDO=∠QBO}\\{DO=BO}\\{∠POD=∠QOB}\end{array}\right.$,
∴△PDO≌△QBO(ASA),
∴OP=OQ;
(2)由题意知:AD=8cm,AP=tcm,
∴PD=8-t,
(3)∵PB=PD,
∴PB2=PD2,
即AB2+AP2=PD2,
∴62+t2=(8-t)2,
解得 t=$\frac{7}{4}$,
∴当t=$\frac{7}{4}$时,PB=PD.
点评 此题考查了菱形的性质与判定、全等三角形的判定与性质以及矩形的性质.注意利用AB2+AP2=PD2,得方程62+t2=(8-t)2是解此题的关键.

练习册系列答案
相关题目
9.如果$\frac{3x}{{x}^{2}-3x}$=$\frac{3}{x-3}$,则x应满足的条件是( )
| A. | x≠0 且x≠3 | B. | x≠0或x≠3 | C. | x>0 | D. | x≠0 |
8.某校学生参加体育测试,某小组10名同学的完成引体向上的个数如下表,
这10名同学引体向上个数的众数与中位数依次是( )
| 完成引体向上的个数 | 10 | 9 | 8 | 7 |
| 人 数 | 1 | 1 | 3 | 5 |
| A. | 7和7.5 | B. | 7和8 | C. | 7.5和9 | D. | 8和9 |
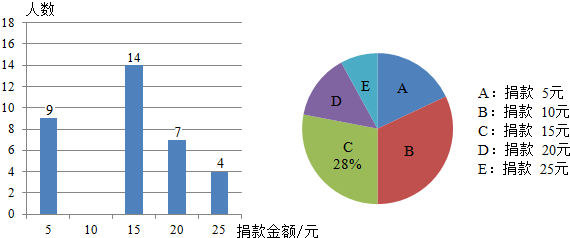
 如图,已知AB∥EF,AC、CE交于点C,求∠BAC+∠ACE+∠CEF的度数.
如图,已知AB∥EF,AC、CE交于点C,求∠BAC+∠ACE+∠CEF的度数.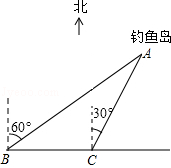 如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行50海里与钓鱼岛A的距离最近?
如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行50海里与钓鱼岛A的距离最近?