题目内容
16．
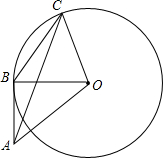如图，AB是⊙O的切线，BC是⊙O的弦，且AB=BC=OB，求∠BAC的度数．
分析 由AB是⊙O的切线，得到∠OBA=90°，根据BC=OB，得到△BOC是等边三角形，这样就得到了∠ABC=150°，再根据等腰三角形的性质求出结果．
解答 解：∵AB是⊙O的切线，
∴∠OBA=90°，
∵BC=OB，
∴BC=OB=OC，
∴∠CBO=60°，
∴∠ABC=150°，
∵AB=BC，
∵∠BAC=$\frac{180°-150°}{2}$=15°．
点评 本题考查了切线的性质，等边三角形的性质，等腰三角形的性质，熟记同圆的半径相等是解题的关键．
练习册系列答案
相关题目
对于一个三角形，设其三个内角的度数分别为x°、y°和z°，若x、y、z满足x2+y2=z2，我们定义这个三角形为美好三角形．
7．下列命题的逆命题是假命题的是（ ）
| A． | 两直线平行，同位角相等 | B． | 平行四边形的对角线互相平分 | ||
| C． | 菱形的四条边相等 | D． | 正方形的四个角都是直角 |
4．在等式a•a2•（ ）=a11中，括号里填入的代数式应当是（ ）
| A． | a7 | B． | a8 | C． | a6 | D． | a3 |
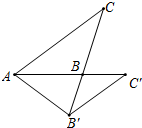如图，△ABC中，∠ABC＞90°，tan∠BAC=$\frac{3}{4}$，BC=4，将三角形绕着点A旋转，点C落在直线AB上的点C′处，点B落在点B′处．若C、B、B′恰好在一直线上，则AB的长为$\frac{6\sqrt{10}}{5}$．
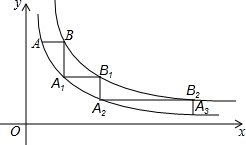如图，在平面直角坐标系的第一象限中，y1=$\frac{4}{x}$和y2=$\frac{8}{x}$，点A（1，a）在y1=$\frac{4}{x}$上，AB∥x轴交y2=$\frac{8}{x}$于点B，BA1∥y轴交y1=$\frac{4}{x}$于点A1，A1B1∥x轴交y2=$\frac{8}{x}$于点B2，…，按照此规律作图，则B2的点坐标为（8，1）．
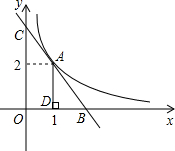直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$只有一个交点A（1，2），且与x轴y轴分别交于B、C两点，AD垂直平分OB，垂足为D，则直线BC的解析式为y=-2x+4．