题目内容
11.正方形ABCD中,点E在边DC上,DE=2,EC=1,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则FC=1或5.分析 分两种情况进行讨论:点F在线段BC上,点F在CB的延长线上,分别根据Rt△ADE≌Rt△ABF(HL),得到BF=DE=2,再根据线段的和差关系进行计算,即可得到CF的长.
解答 解:①如图所示,当点F在线段BC上时,
由题意可得,AF=AE,AB=AD,∠D=∠ABF=90°,
在Rt△ADE和Rt△ABF中,
$\left\{\begin{array}{l}{AE=AF}\\{AD=AB}\end{array}\right.$,
∴Rt△ADE≌Rt△ABF(HL),
∴BF=DE=2,
又∵BC=DC,
∴CF=CE=1;
②如图所示,当点F在CB的延长线上时,
由题意可得,AF=AE,AB=AD,∠D=∠ABF=90°,
在Rt△ADE和Rt△ABF中,
$\left\{\begin{array}{l}{AE=AF}\\{AD=AB}\end{array}\right.$,
∴Rt△ADE≌Rt△ABF(HL),
∴BF=DE=2,
又∵BC=DC=3,
∴CF=2+3=5.
故答案为:1或5.
点评 本题主要考查了旋转的性质以及正方形的性质的运用,解决问题的关键是依据全等三角形的对应边相等以及正方形的四条边相等进行计算.

练习册系列答案
相关题目
1.a、b、c是三角形的三边长,且(a+b)2=c2+2ab,则这个三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
1.方程x2-2=0的解为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 2或-2 | D. | $\sqrt{2}$或-$\sqrt{2}$ |
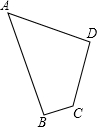 如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.