题目内容
2.太原双塔寺又名永祚寺,是国家级文物保护单位,由于双塔(舍利塔、文峰塔)耸立,被人们称为“文笔双塔”,是太原的标志性建筑之一,某校社会实践小组为了测量舍利塔的高度,在地面上的C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,舍利塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点C处,这时地面上的点F,标杆的顶端点H,舍利塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米.请你根据以上数据,计算舍利塔的高度AB.
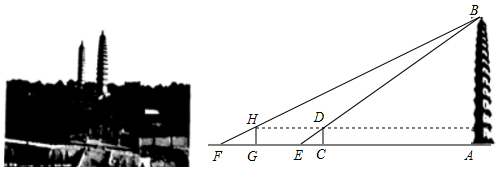
分析 易知△EDC∽△EBA,△FHC∽△FBA,可得$\frac{GH}{BA}$=$\frac{FG}{FA}$,$\frac{DC}{BA}$=$\frac{EC}{EA}$,因为DC=HG,推出$\frac{FG}{FA}$=$\frac{EC}{EA}$,列出方程求出CA=106(米),由$\frac{DC}{BA}$=$\frac{EC}{EA}$,可得$\frac{2}{BA}$=$\frac{4}{4+106}$,由此即可解决问题.
解答 解:∵△EDC∽△EBA,△FHC∽△FBA,
∴$\frac{GH}{BA}$=$\frac{FG}{FA}$,$\frac{DC}{BA}$=$\frac{EC}{EA}$,∵DC=HG,
∴$\frac{FG}{FA}$=$\frac{EC}{EA}$,
∴$\frac{6}{59+CA}$=$\frac{4}{4+CA}$,
∴CA=106(米),
∵$\frac{DC}{BA}$=$\frac{EC}{EA}$,
∴$\frac{2}{BA}$=$\frac{4}{4+106}$,
∴AB=55(米),
答:舍利塔的高度AB为55米.
点评 本题考查解直角三角形的应用、相似三角形的判定和性质,解题的关键是灵活运用所学知识解决问题,学会构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
13.己知a是方程x2-3x-1=0的一个根,则代数式2a2-6a+3的值是( )
| A. | 6 | B. | 5 | C. | $12+2\sqrt{13}$ | D. | $12-2\sqrt{13}$ |
17.已知△ABC的三边a=m-n(m>n>0),b=m+n,c=2$\sqrt{mn}$.
(1)求证:△ABC是直角三角形;
(2)利用第(1)题的结论,写出两组m,n的值,要求三角形的边长均为整数.
(1)求证:△ABC是直角三角形;
(2)利用第(1)题的结论,写出两组m,n的值,要求三角形的边长均为整数.
14.已知2a>3b,则下列不等式中,正确的是( )
| A. | -8a>-12b | B. | 4a<6b | C. | 1-2a>1-3b | D. | 2a-1>3b-1 |
12.要使方程x2-mx+m=-1有实数根,实数m的值可以是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 5 |
 如图是由12个边长为1的小正方形拼成的,请连结这些小正方形的两个顶点,得到一个长为5的线段.
如图是由12个边长为1的小正方形拼成的,请连结这些小正方形的两个顶点,得到一个长为5的线段.